
 .再由 f′(1)=0,利用函数的周期性求出方程f′(x)=0在区间[0,6]上的实根,从而得出结论.
.再由 f′(1)=0,利用函数的周期性求出方程f′(x)=0在区间[0,6]上的实根,从而得出结论. )=f(x-
)=f(x- )=f(
)=f( -x),
-x), 对称,且函数f′(x)是奇函数,且周期等于
对称,且函数f′(x)是奇函数,且周期等于 .
. )=f'(3)=0.
)=f'(3)=0. 以及 f′(1)=0,求得 f′(
以及 f′(1)=0,求得 f′( )=f′(4)=f′(
)=f′(4)=f′( )=f′(
)=f′(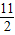 )=f′(6)=0.
)=f′(6)=0. ,1,
,1, ,3,4,
,3,4, ,
,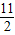 ,6,共有9个,
,6,共有9个,

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com