
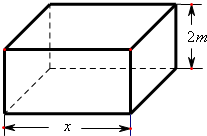
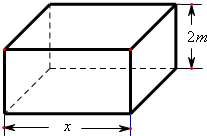
 现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.
现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.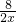 =
= m,
m, )×2=(4x+
)×2=(4x+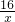 )(m2),S底=4(m2),
)(m2),S底=4(m2),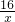 )+80×4=480x+
)+80×4=480x+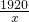 +320(元)(x>0).
+320(元)(x>0).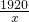 +320≥2
+320≥2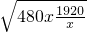 +320=960×2+320=2240(元).(当且仅当x=2时取“=”).
+320=960×2+320=2240(元).(当且仅当x=2时取“=”). m,利用池底和池壁的造价分别为120元/m2和80元/m2可求得函数解析式y=f(x)及x的取值范围;
m,利用池底和池壁的造价分别为120元/m2和80元/m2可求得函数解析式y=f(x)及x的取值范围;

科目:高中数学 来源: 题型:
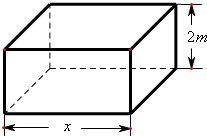 现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.
现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com