
【题目】设a , b , c为正数,且不全相等.求证:![]() .
.
【答案】证明:本题考查三维形式的柯西不等式的应用.解答本题需要构造两组数据 ![]() ,
, ![]() ,
, ![]() ;
;![]()
![]() ,
,![]() ,然后利用柯西不等式解决.
,然后利用柯西不等式解决.
构造两组数 ![]() ,
, ![]() ,
, ![]() ;
;![]()
![]() ,
,![]() ,则由柯西不等式得
,则由柯西不等式得![]() ,①
,①
即![]() ,
,
于是![]() .
.
由柯西不等式知,①中有等号成立![]() .
.
因题设,a , b , c不全相等,故①中等号不成立,
于是 ![]() .
.
【解析】本题主要考查了一般形式的柯西不等式,解决问题的关键是柯西不等式的结构特征可以记为 ![]() ,其中ai , bi∈R+(i=1,2,…,n),在使用柯西不等式时(要注意从整体上把握柯西不等式的结构特征),准确地构造公式左侧的两个数组是解决问题的关键.
,其中ai , bi∈R+(i=1,2,…,n),在使用柯西不等式时(要注意从整体上把握柯西不等式的结构特征),准确地构造公式左侧的两个数组是解决问题的关键.
【考点精析】关于本题考查的一般形式的柯西不等式,需要了解一般形式的柯西不等式:![]()
![]() 才能得出正确答案.
才能得出正确答案.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,且a=2bsin A. (Ⅰ)求角B的大小;
(Ⅱ)若a= ![]() ,c=5,求△ABC的面积及b.
,c=5,求△ABC的面积及b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( ) 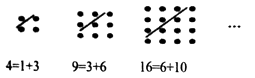
A.16=3+13
B.25=9+16
C.36=10+26
D.49=21+28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+2|+|x﹣2|<18的解集为A.
(1)求A;
(2)若a,b∈A,x∈(0,+∞),不等式a+b<x ![]() +m恒成立,求实数m的取值范围.
+m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com