
【题目】在平面直角坐标系![]() 中,曲线
中,曲线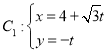 (t为参数),曲线
(t为参数),曲线![]() ,(
,(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 分别交
分别交![]() ,
,![]() 于A,B两点,求
于A,B两点,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() 在底面
在底面![]() 上的投影为
上的投影为![]() 的中点
的中点![]() ,
,![]() .有下列结论:
.有下列结论:
①三棱锥![]() 的三条侧棱长均相等;
的三条侧棱长均相等;
②![]() 的取值范围是
的取值范围是![]() ;
;
③若三棱锥的四个顶点都在球![]() 的表面上,则球
的表面上,则球![]() 的体积为
的体积为![]() ;
;
④若![]() ,
,![]() 是线段
是线段![]() 上一动点,则
上一动点,则![]() 的最小值为
的最小值为![]() .
.
其中所有正确结论的编号是( )
A.①②B.②③C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,E是
,E是![]() 的中点.现将
的中点.现将![]() 沿
沿![]() 翻折,使点A移动至平面
翻折,使点A移动至平面![]() 外的点P.
外的点P.
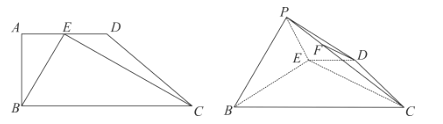
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
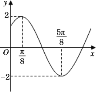
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治疗某种疾病,某科研机构研制了甲、乙两种新药,为此进行白鼠试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药一轮的治疗结果得出后,再安排下一轮试验.4轮试验后,就停止试验.甲、乙两种药的治愈率分别是![]() 和
和![]() .
.
(1)若![]() ,求2轮试验后乙药治愈的白鼠比甲药治愈的白鼠多1只的概率;
,求2轮试验后乙药治愈的白鼠比甲药治愈的白鼠多1只的概率;
(2)已知A公司打算投资甲、乙这两种新药的试验耗材费用,甲药和乙药一次试验耗材花费分别为3千元和![]() 千元,每轮试验若甲、乙两种药都治愈或都没有治愈,则该科研机构和A公司各承担该轮试验耗材总费用的50%;若甲药治愈,乙药未治愈,则A公司承担该轮试验耗材总费用的75%,其余由科研机构承担,若甲药未治愈,乙药治愈,则A公司承担该轮试验耗材总费用的25%,其余由科研机构承担.以A公司每轮支付试验耗材费用的期望为标准,求A公司4轮试验结束后支付试验耗材最少费用为多少元?
千元,每轮试验若甲、乙两种药都治愈或都没有治愈,则该科研机构和A公司各承担该轮试验耗材总费用的50%;若甲药治愈,乙药未治愈,则A公司承担该轮试验耗材总费用的75%,其余由科研机构承担,若甲药未治愈,乙药治愈,则A公司承担该轮试验耗材总费用的25%,其余由科研机构承担.以A公司每轮支付试验耗材费用的期望为标准,求A公司4轮试验结束后支付试验耗材最少费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为椭圆
为椭圆![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,设
,设![]() 的角平分线
的角平分线![]() 交椭圆
交椭圆![]() 的长轴于点
的长轴于点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com