
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的最大值和最小值;
(2)当a∈R时,求函数f(x)的最小值.
【答案】
(1)解:当a=﹣1时,函数f(x)=x2﹣2x+2的图象是开口朝上,且以直线x=1为对称轴的抛物线,
由x∈[﹣5,5]得:
x=﹣5时,函数取最大值37,
x=1时,函数取最小值1
(2)解:函数f(x)=x2+2ax+2的图象是开口朝上,且以直线x=﹣a为对称轴的抛物线,
若﹣a<﹣5,即a>5,函数f(x)在[﹣5,5]上为增函数,
当x=﹣5时,函数取最小值27﹣10a;
若﹣5≤﹣a≤5,即﹣5≤a≤5,函数f(x)在[﹣5,﹣a]上为减函数,在[﹣a,5]上为增函数,
当x=﹣a时,函数取最小值2﹣a2;
若﹣a>5,即a<﹣5,函数f(x)在[﹣5,5]上为减函数,
当x=5时,函数取最小值27+10a.
综上可得:函数f(x)的最小值为: 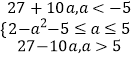
【解析】(1)当a=﹣1时,函数f(x)=x2﹣2x+2的图象是开口朝上,且以直线x=1为对称轴的抛物线,进而可得函数f(x)的最大值和最小值;(2)函数f(x)=x2+2ax+2的图象是开口朝上,且以直线x=﹣a为对称轴的抛物线,分类讨论对称轴与给定区间的位置关系,综合讨论结果,可得答案.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】给出下列结论:
①y=x2+1,x∈[﹣1,2],y的值域[2,5]是;
②幂函数图象一定不过第四象限;
③函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
④若loga ![]() >1,则a的取值范围是(
>1,则a的取值范围是( ![]() ,1);
,1);
⑤函数f(x)= ![]() +
+ ![]() 是既奇又偶的函数;
是既奇又偶的函数;
其中正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
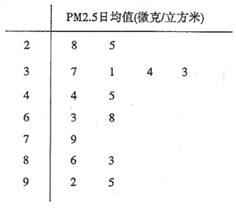
(1)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(2)从这15天的数据中任取3天的数据,记![]() 表示其中空气质量达到一级的天数,求
表示其中空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合U=R,A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求A∩B,(UA)∪B;
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:①y=1是幂函数;
②定义在R上的奇函数y=f(x)满足f(0)=0
③函数 ![]() 是奇函数
是奇函数
④当a<0时, ![]()
⑤函数y=1的零点有2个;
其中正确结论的序号是(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC﹣A1B1C1的所有棱长都为2,D为CC1中点.试用空间向量知识解下列问题: 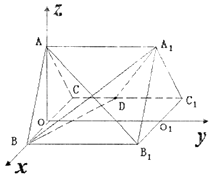
(1)求证:平面ABB1A1⊥平面A1BD;
(2)求二面角A﹣A1D﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com