已知集合A={-1.0.1}.B={x|x2-x+1}.若A∪B=A.则x=0或1．题目和参考答案——青夏教育精英家教网—

14．已知集合A={-1，0，1}，B={x|x²-x+1}，若A∪B=A，则x=0或1．

分析根据A，B，以及A与B的并集为A，确定出x的值即可．

解答解：∵A={-1，0，1}，B={x|x²-x+1}，且A∪B=A，
∴x²-x+1=-1或x²-x+1=0或x²-x+1=1，
解得：无解；无解；x=0或x=1，
把x=0代入B中代数式得：原式=1；把x=1代入B中代数式得：原式=1，
则x=0或1，
故答案为：0或1．

点评此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

4．设全集U=R，集合A={x|x²+x-2＞0}，B={y|y=2^x，x∈R}，则A∩B={x|x＞1}A∪B={x|x＜-2或x＞0}，∁_UA={x|-2≤x≤1}．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．计算：3+4×2¹+4×2²+4×2³+…+4×2^n-1-（4n-1）2ⁿ．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．当x取何值时，函数y=tan²x-2tanx+3达到最小值，并求出最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．设函数f（x）=3ax²-2（a+c）x+c（a＞0，a，c∈R）
（1）设a＞c＞0，若f（x）＞c²-2c+a对x∈[1，+∞]恒成立，求c的取值范围；
（2）函数f（x）在区间（0，1）内是否有零点，有几个零点？为什么？

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

19．函数y=$\frac{{\sqrt{8-2x}}}{{{{log}_2}（3x+1）}}$的定义域是{x|-$\frac{1}{3}$＜x≤4，且x≠0}．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．

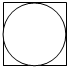在如图的正方形中随机撒一把豆子，用随机模拟的方法估圆周率的值：经查数，落在正方形中的豆子的总数为n粒，其中m（m＜n）粒豆子落在该正方形的内切圆内，以此估计圆周率π为（　　）

A．

$\frac{m}{n}$

B．

$\frac{2m}{n}$

C．

$\frac{3m}{n}$

D．

$\frac{4m}{n}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．

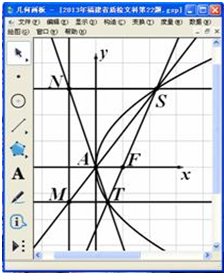某同学用《几何画板》研究抛物线的性质：打开《几何画板》软件，绘制某抛物线E：y²=2px，在抛物线上任意画一个点S，度量点S的坐标（x_S，y_S），如图．
（Ⅰ）拖动点S，发现当x_S=4时，y_S=4，试求抛物线E的方程；
（Ⅱ）设抛物线E的顶点为A，焦点为F，构造直线SF交抛物线E于不同两点S、T，构造直线AS、AT分别交准线于M、N两点，构造直线MT、NS．经观察得：沿着抛物线E，无论怎样拖动点S，恒有MT∥NS．请你证明这一结论．
（Ⅲ）为进一步研究该抛物线E的性质，某同学进行了下面的尝试：在（Ⅱ）中，把“焦点F”改变为其它“定点G（g，0）（g≠0）”，其余条件不变，发现“MT与NS不再平行”．是否可以适当更改（Ⅱ）中的其它条件，使得仍有“MT∥NS”成立？如果可以，请写出相应的正确命题；否则，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．已知函数f（x）=$\frac{1}{2}$x²+2ax，g（x）=3a²lnx+b．
（1）设两曲线y=f（x）与y=g（x）有公共点，且在公共点处的切线相同，若a＞0，试建立b关于的函数关系式；
（2）若任意b∈[0，2]，h（x）=f（x）+g（x）-（2a+b）x在（0，4）上为单调函数，求a的取值范围．
（3）a=-1，b=0，设正项数列{a_n}（n∈N^*）满足a₁=a（a＞0），g（a_n+1）=f（a_n），证明：存在常数M，使得对于任意的n∈N^*，都有a_n≤M．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学