
【题目】已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为![]() 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线AP与椭圆在点B处的切线交于点D,当点P在椭圆上运动时,求证:以BD为直径的圆与直线PF恒相切.
【答案】(Ⅰ)椭圆C的方程为![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(1)根据题意得到a,b,c的方程组,解方程组即得椭圆C的方程.(2)求证圆心到直线PF的距离等于![]() |BD|,即证以BD为直径的圆与直线PF恒相切.
|BD|,即证以BD为直径的圆与直线PF恒相切.
(1)由题意可设椭圆C的方程为![]() (a>b>0),F(c,0).
(a>b>0),F(c,0).
由题意知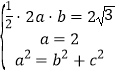 ,解得b=
,解得b=![]() ,c=1.
,c=1.
故椭圆C的方程为![]() ,离心率为
,离心率为![]() 。
。
(2)证明:由题意可设直线AP的方程为y=k(x+2)(k≠0)。
则点D坐标为(2,4k),BD中点E的坐标为(2,2k).
由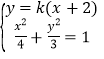 得
得![]()
设点P的坐标为![]() ,则
,则![]()
所以![]()
因为点F坐标为(1,0),
当k=±![]() 时,点P的坐标为
时,点P的坐标为![]() ,直线PF⊥x轴,点D的坐标为(2,±2).
,直线PF⊥x轴,点D的坐标为(2,±2).
此时以BD为直径的圆![]() (与直线PF相切.
(与直线PF相切.
当![]() 时,则直线PF的斜率
时,则直线PF的斜率![]() ,
,
所以直线PF的方程为![]() ,
,
点E到直线PF的距离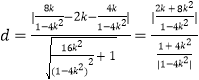
又因为|BD|=4|k|,所以d=![]() |BD|.
|BD|.
故以BD为直径的圆与直线PF相切.
综上得,当点P在椭圆上运动时,以BD为直径的圆与直线PF恒相切.


科目:高中数学 来源: 题型:
【题目】传说《西游记》中孙悟空的“如意金箍棒”原本是东海海底的一枚“定海神针”.作为兵器,“如意金箍棒”威力巨大,且只有孙悟空能让其大小随意变化。假定孙悟空在使用“如意金箍棒”与各路妖怪打斗时,都将其变化为底面半径为4![]() 至10
至10![]() 之间的圆柱体。现假定孙悟空刚与一妖怪打斗完毕,并降伏了此妖怪,此时“如意金箍棒”的底面半径为10
之间的圆柱体。现假定孙悟空刚与一妖怪打斗完毕,并降伏了此妖怪,此时“如意金箍棒”的底面半径为10![]() ,长度为
,长度为![]() .在此基础上,孙悟空使“如意金箍棒”的底面半径以每秒1
.在此基础上,孙悟空使“如意金箍棒”的底面半径以每秒1![]() 匀速缩短,同时长度以每秒40
匀速缩短,同时长度以每秒40![]() 匀速增长,且在这一变化过程中,当“如意金箍棒”的底面半径为8
匀速增长,且在这一变化过程中,当“如意金箍棒”的底面半径为8![]() 时,其体积最大.
时,其体积最大.
(1)求在这一变化过程中,“如意金箍棒”的体积![]() 随时间
随时间![]() (秒)变化的解析式,并求出其定义域;
(秒)变化的解析式,并求出其定义域;
(2)假设在这一变化过程中,孙悟空在“如意金箍棒”体积最小时,将其定型,准备迎战下一个妖怪。求此时“如意金箍棒”的底面半径。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和抛物线
和抛物线![]() ,圆
,圆![]() 与抛物线
与抛物线![]() 的准线交于
的准线交于![]() 、
、![]() 两点,
两点,![]() 的面积为
的面积为![]() ,其中
,其中![]() 是
是![]() 的焦点.
的焦点.
(1)求抛物线![]() 的方程;
的方程;
(2)不过原点![]() 的动直线
的动直线![]() 交该抛物线于
交该抛物线于![]() ,
,![]() 两点,且满足
两点,且满足![]() ,设点
,设点![]() 为圆
为圆![]() 上任意一动点,求当动点
上任意一动点,求当动点![]() 到直线
到直线![]() 的距离最大时直线
的距离最大时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是甲、乙两名射击运动员在参赛前的训练中击中10环以上的次数统计,根据表格中的数据回答以下问题:
射击次数 | 10 | 20 | 50 | 100 | 200 | 500 |
甲击中10环以上的次数 | 9 | 17 | 44 | 92 | 179 | 450 |
甲击中10环以上的频率 |
射击次数 | 10 | 20 | 50 | 100 | 200 | 500 |
乙击中10环以上的次数 | 8 | 19 | 44 | 93 | 177 | 453 |
乙击中10环以上的频率 |
(1)分别计算出两位运动员击中10环以上的频率;
(2)根据(l)中的计算结果预测两位运动员在比赛时击中10环以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购450件服装时,该服装厂获得的利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以5cm为单位长度作单位圆,分别作出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 角的正弦线余弦线和正切线,量出它们的长度,写出这些角的正弦余弦和正切的近似值,再使用科学计算器求这些角的正弦余弦和正切,并进行比较.
角的正弦线余弦线和正切线,量出它们的长度,写出这些角的正弦余弦和正切的近似值,再使用科学计算器求这些角的正弦余弦和正切,并进行比较.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com