
| π |
| 3 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
D、-
|
科目:高中数学 来源:2011-2012学年河南省豫东、豫北十所名校高三测试理科数学试卷(解析版) 题型:选择题
我们把正切函数在整个定义域内的图象看作一组“平行曲线”,而“平行曲线”具有性质:任意两条平行于横轴的直线与两条相邻的“平行曲线”相交,被截得的线段长度相等,已知函数 图象中的两条相邻“平行曲线”与直线y =2012相交于A,B两点,且|AB| =2,则
图象中的两条相邻“平行曲线”与直线y =2012相交于A,B两点,且|AB| =2,则 )=
)=
A. B.
B.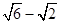 C.
C.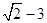 D.-
D.-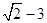
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com