
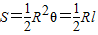 ,l表示扇形的弧长)
,l表示扇形的弧长)
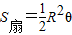 ,
, ,
, .
. ,
, ,
, ,
,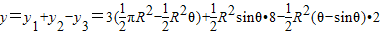 .=
.=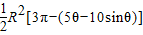
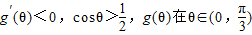 上为减函数;
上为减函数;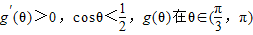 上为增函数.
上为增函数. 时,g(θ)取到最小值,此时总利润最大.
时,g(θ)取到最小值,此时总利润最大. 时,总利润最大.
时,总利润最大.

科目:高中数学 来源: 题型:
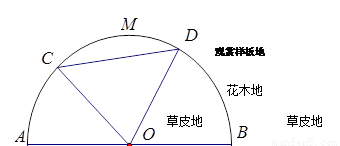
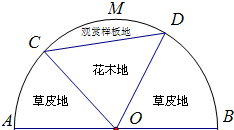 某园林公司计划在一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
某园林公司计划在一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2014届广东佛山佛山一中高二下第一次段考文科数学试卷(解析版) 题型:解答题
某园林公司计划在一块 为圆心,
为圆心,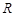 (
(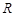 为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形
为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形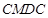 区域用于观赏样板地,
区域用于观赏样板地,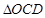 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.

(1)设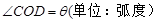 , ,用
, ,用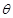 表示弓形
表示弓形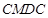 的面积
的面积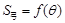 ;
;
(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的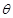
(参考公式:扇形面积公式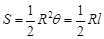 ,
,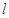 表示扇形的弧长)
表示扇形的弧长)
查看答案和解析>>
科目:高中数学 来源:2013届河北衡水中学高二第二学期期末理科数学试卷(解析版) 题型:解答题
(本题满分14分)某园林公司计划在一块 为圆心,
为圆心,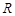 (
(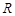 为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形
为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形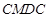 区域用于观赏样板地,
区域用于观赏样板地,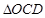 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.

(1)设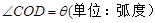 , 用
, 用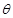 表示弓形
表示弓形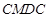 的面积
的面积 ;(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的
;(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的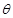
(参考公式:扇形面积公式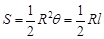 ,
,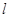 表示扇形的弧长)
表示扇形的弧长)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三第四次月考数学理卷 题型:解答题
(本小题满分13分)某园林公司计划在一块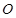 为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形
为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形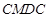 区域用于观赏样板地,
区域用于观赏样板地,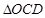 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1) 设 ,
,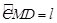 ,分别用
,分别用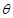 ,
,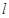 表示弓形
表示弓形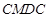 的面积
的面积 ;
;




|
 (2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式
(2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式 )
)
 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省、华师附中、深圳中学、广雅中学高三上学期期末数学理卷 题型:解答题
((本题满分14分)
某园林公司计划在一块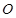 为圆心,
为圆心, (
( 为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形
为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形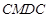 区域用于观赏样板地,
区域用于观赏样板地,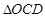 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1)设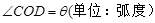 , ,用
, ,用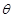 表示弓形
表示弓形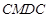 的面积
的面积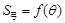 ;
;
(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的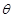
(参考公式:扇形面积公式 ,
,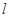 表示扇形的弧长)
表示扇形的弧长)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com