
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)绝对值函数分段讨论解不等式。(2)由题意可得函数f(x)的值域是函数g(x)值域的子集,所以先求得f(x)的值域,再由绝对值不等式求得g(x)值域。
试题解析:(Ⅰ)不等式f(x)>9![]() ,或
,或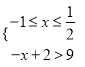 ,或
,或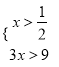 ,
,
即x<﹣3或∈或x>3,∴原不等式解集为(3,+∞)∪(﹣∞,3);
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2)函数f(x)的值域是函数g(x)值域的子集, 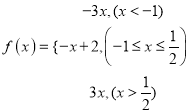 ,当x<﹣1时,﹣3x>3;
,当x<﹣1时,﹣3x>3;
当﹣1≤x![]() 时,
时, ![]() ﹣x+2≤3;当
﹣x+2≤3;当![]() 时,
时, ![]() ,
,
∴函数f(x)的值域是![]() ,g(x)=|x﹣a|+|x+a|≥|2a|,
,g(x)=|x﹣a|+|x+a|≥|2a|,
∴![]() ,即
,即![]() .∴实数a的取值范围为[﹣
.∴实数a的取值范围为[﹣![]() ,
, ![]() ].
].


科目:高中数学 来源: 题型:
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“ 25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

附表:
P( | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
![]() ,(其中
,(其中 ![]() )
)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 ![]() 的列联表,并判断是否有
的列联表,并判断是否有 ![]() 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法: ①线性回归分析就是由样本点去寻找一条直线,使之贴近这些样本点的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归方程 ![]() ,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验.其中正确命题的个数是( )
,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验.其中正确命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论,其中正确的个数为( ). ①已 ![]() ,则
,则 ![]()
②过原点作曲线 ![]() 的切线,则切线方程为
的切线,则切线方程为 ![]() (其中e为自然对数的底数);
(其中e为自然对数的底数);
③已知随机变 ![]()
![]() ,则
,则 ![]()
④已知n为正偶数,用数学归纳法证明等式 ![]() 时,若假设
时,若假设 ![]() 时,命题为真,则还需利用归纳假设再证明
时,命题为真,则还需利用归纳假设再证明 ![]() 时等式成立,即可证明等式对一切正偶数n都成立.
时等式成立,即可证明等式对一切正偶数n都成立.
⑤在回归分析中,常用 ![]() 来刻画回归效果,在线性回归模型中,
来刻画回归效果,在线性回归模型中, ![]() 表示解释变量对于预报变量变化的贡献率
表示解释变量对于预报变量变化的贡献率 ![]() 越接近1,表示回归的效果越好.
越接近1,表示回归的效果越好.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB,☉O交直线OB于E,D两点,连接EC,CD. 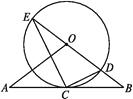
(1)求证:直线AB是☉O的切线;
(2)若tan∠CED= ![]() ,☉O的半径为3,求OA的长.
,☉O的半径为3,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com