已知函数f(x)=2x+1定义在R上.
(1)若f(x)可以表示为一个偶函数g(x)与一个奇函数h(x)之和,设h(x)=t,p(t)=g(2x)+2mh(x)+m2-m-1(m∈R),求出p(t)的解析式;
(2)若p(t)≥m2-m-1对于x∈[1,2]恒成立,求m的取值范围;
(3)若方程p(p(t))=0无实根,求m的取值范围.
解:(1)假设f(x)=g(x)+h(x)①,其中g(x)偶函数,h(x)为奇函数,
则有f(-x)=g(-x)+h(-x),即f(-x)=g(x)-h(x)②,
由①②解得
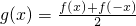
,
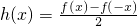
.
∵f(x)定义在R上,∴g(x),h(x)都定义在R上.
∵
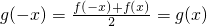
,
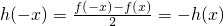
.
∴g(x)是偶函数,h(x)是奇函数,∵f(x)=2
x+1,
∴
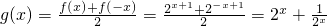
,
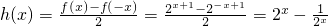
.
由
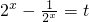
,则t∈R,
平方得
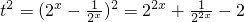
,∴
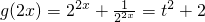
,
∴p(t)=t
2+2mt+m
2-m+1.
(2)∵t=h(x)关于x∈[1,2]单调递增,∴
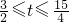
.
∴p(t)=t
2+2mt+m
2-m+1≥m
2-m-1对于
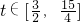
恒成立,
∴

对于
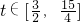
恒成立,
令

,则
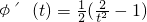
,
∵
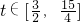
,∴

,故

在
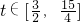
上单调递减,
∴
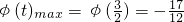
,∴
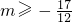
为m的取值范围.
(3)由(1)得p(p(t))=[p(t)]
2+2mp(t)+m
2-m+1,
若p(p(t))=0无实根,即[p(t)]
2+2mp(t)+m
2-m+1①无实根,
方程①的判别式△=4m
2-4(m
2-m+1)=4(m-1).
1°当方程①的判别式△<0,即m<1时,方程①无实根.
2°当方程①的判别式△≥0,即m≥1时,
方程①有两个实根
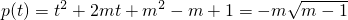
,
即
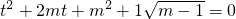
②,
只要方程②无实根,故其判别式
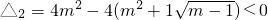
,
即得
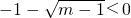
③,且
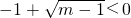
④,
∵m≥1,③恒成立,由④解得m<2,∴③④同时成立得1≤m<2.
综上,m的取值范围为m<2.
分析:(1)利用f(x)=g(x)+h(x)和f(-x)=g(-x)+h(-x)求出g(x)和h(x)的表达式,再求出p(t)关于t的表达式即可.
(2)先有x∈[1,2]找出t的范围,在把所求问题转化为求p(t)在[

,

]的最小值.让大于等于m
2-m-1即可.
(3)转化为关于p(t)的一元二次方程,利用判别式的取值,再分别讨论即可.
点评:本题是在考查指数函数的基础上对函数的恒成立问题,函数奇偶性以及一元二次方程根的判断的综合考查,是一道综合性很强的难题.

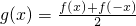 ,
,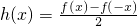 .
.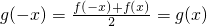 ,
,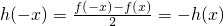 .
.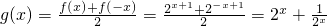 ,
,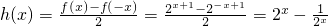 .
.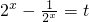 ,则t∈R,
,则t∈R,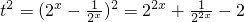 ,∴
,∴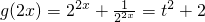 ,
,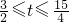 .
.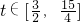 恒成立,
恒成立, 对于
对于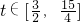 恒成立,
恒成立, ,则
,则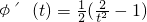 ,
,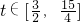 ,∴
,∴ ,故
,故 在
在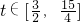 上单调递减,
上单调递减,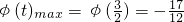 ,∴
,∴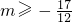 为m的取值范围.
为m的取值范围.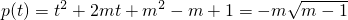 ,
,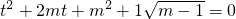 ②,
②,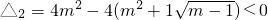 ,
,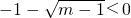 ③,且
③,且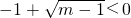 ④,
④, ,
, ]的最小值.让大于等于m2-m-1即可.
]的最小值.让大于等于m2-m-1即可.
