
图2-2-2
思路分析:要证明MN∥α,由于AB、CD为异面直线,所以要在α内找一条直线,证明它与MN平行较为困难,因此可转化为证明过MN的一个平面与平面α平行.
证法一:过点A作AE∥CD,交α于点E,
∵α∥β,则AE![]() CD,即AEDC为平行四边形.
CD,即AEDC为平行四边形.
设P为AE的中点,连结PN、PM、BE,
则PN∥ED,MP∥BE.
又∵PN![]() α,ED
α,ED![]() α,∴PN∥α.
α,∴PN∥α.
同理可得,PM∥α.
又∵PM∩PN=P,
∴平面PMN∥平面α.
又MN![]() 平面PMN,
平面PMN,
∴MN∥α.
证法二:如图2-2-3所示,连结AD,取AD的中点Q,连结QM、QN,
∵Q、N分别为AD、CD的中点,∴QN∥AC.
∵QN![]() β,AC
β,AC![]() β,
β,
∴QN∥β.
∵α∥β,QN∥β,QN![]() α,
α,

图2-2-3
∴QN∥α,同理可证QM∥α.
∵QM∩QN=Q,∴平面QMN∥α.
∵MN![]() 平面MNQ.∴MN∥α.
平面MNQ.∴MN∥α.
绿色通道:
本题的证法较多,解题关键是如何处理好条件:AB、CD是两条异面线段.证法一实质上是把CD在两平行平面间沿着同一方向移到AE位置,AB和AE可确定一平面,借助于平面几何来处理问题;证法二是借助于空间四边形的对角线AD,把AB和CD分别放在两相交平面内来研究.本题还可以连结CM,延长交α于点R,证明MN∥RD即可.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
图2-2-14
查看答案和解析>>
科目:高中数学 来源: 题型:
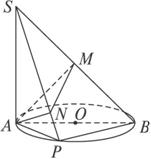
图2-2-2
(1)△SPB是直角三角形;
(2)AN⊥平面SPB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com