
【题目】下列命题
①命题“若![]() ,则
,则![]() ”的逆命题是真命题;
”的逆命题是真命题;
②若![]() ,
,![]() ,则
,则![]() 在
在![]() 上的投影是
上的投影是![]() ;
;
③在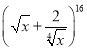 的二项展开式中,有理项共有4项;
的二项展开式中,有理项共有4项;
④已知一组正数![]() ,
,![]() ,
,![]() ,
,![]() 的方差为
的方差为![]() ,则数据
,则数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数为4;
的平均数为4;
⑤复数![]() 的共轭复数是
的共轭复数是![]() ,则
,则![]() .
.
其中真命题的个数为( )
A.0B.1C.2D.3
【答案】B
【解析】
①、写出原命题的逆命题,并利用特殊值判断①不正确;②、计算出![]() 在
在![]() 上的投影,由此判断②不正确;③利用二项式展开式的通项公式求得有理项,由此判断③错误;④、利用方差的计算公式、平均数的计算公式,判断④正确;⑤化简
上的投影,由此判断②不正确;③利用二项式展开式的通项公式求得有理项,由此判断③错误;④、利用方差的计算公式、平均数的计算公式,判断④正确;⑤化简![]() 并求得其共轭复数,由此求得
并求得其共轭复数,由此求得![]() ,判断⑤不正确.
,判断⑤不正确.
根据题意,依次分析命题:
①,命题“若![]() ,则
,则![]() ”的逆命题为“若
”的逆命题为“若![]() ,则
,则![]() ”,当
”,当![]() 时,命题不成立,则①不正确;
时,命题不成立,则①不正确;
②![]() 在
在![]() 上的投影是
上的投影是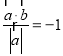 ,则②不正确;
,则②不正确;
③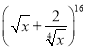 的展开式通项为
的展开式通项为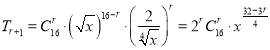 ,当
,当![]() 时,为有理项,则其有理项共3项,则③错误;
时,为有理项,则其有理项共3项,则③错误;
④根据题意,由方差的计算公式![]() ,而这组数据的方差为
,而这组数据的方差为![]() ,则这组数据
,则这组数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数为2,即
的平均数为2,即![]() ,则
,则![]() ,那么数据
,那么数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数为
的平均数为![]()
![]() ,则④正确;
,则④正确;
⑤复数![]() ,则其共轭复数是
,则其共轭复数是![]() ,则
,则![]() ,
,![]() ,有
,有![]() ,则⑤不正确;
,则⑤不正确;
有1个命题正确;
故选:B.


科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为周期函数,证明:
为周期函数,证明:![]() 是常值函数;
是常值函数;
(3)若![]()
①记![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
②求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.

(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,某市工会组织部分事业单位职工举行“迎国庆,广播操比赛”活动.现有200名职工参与了此项活动,将这200人按照年龄(单位:岁)分组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的频率分布直方图如图所示.记事件A为“从这200人中随机抽取一人,其年龄不低于35岁”,已知P(A)=0.75.
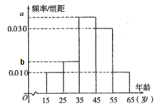
(1)求![]() 的值;
的值;
(2)在第二组、第四组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人作为活动的负责人,求这2人恰好都在第四组中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正数数列![]() 、
、![]() 满足:
满足:![]() ≥
≥![]() ,且对一切k≥2,k
,且对一切k≥2,k![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,
的等差中项,![]() 是
是![]() 与
与![]() 的等比中项.
的等比中项.
(1)若![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)求证:![]() 是等差数列的充要条件是
是等差数列的充要条件是![]() 为常数数列;
为常数数列;
(3)记![]() ,当n≥2(n
,当n≥2(n![]() )时,指出
)时,指出![]() 与
与![]() 的大小关系并说明理由.
的大小关系并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的一个焦点
)的一个焦点![]() 与抛物线
与抛物线![]() :
:![]() 的焦点重合,且离心率为
的焦点重合,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,满足
两点,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谈祥柏先生是我国著名的数学科普作家,他写的《数学百草园》、《好玩的数学》、《故事中的数学》等书,题材广泛、妙趣横生,深受广大读者喜爱.下面我们一起来看《好玩的数学》中谈老的一篇文章《五分钟内挑出埃及分数》:文章首先告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).如用两个埃及分数![]() 与
与![]() 的和表示
的和表示![]() 等.从
等.从![]() 这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com