
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
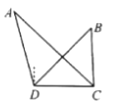
【题目】如图所示,为了测量A、B处岛屿的距离,小海在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶20海里至C处,观测B在C处的正北方向,A在C处的北偏西45°方向,则A、B两岛屿的距高为___________海里.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若![]() ,关于
,关于![]() 的方程
的方程![]() 有且仅有一个根, 求实数
有且仅有一个根, 求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,不等式
,不等式![]() 均成立, 求实数
均成立, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() ,
,![]() 满足:
满足:![]() ,且
,且![]() ,
,![]() ,并且当
,并且当![]() 时,
时,![]() .给出如下结论:①函数
.给出如下结论:①函数![]() 是偶函数;②函数
是偶函数;②函数![]() 在
在![]() 上单调递增;③函数
上单调递增;③函数![]() 是以2为周期的周期函数;④
是以2为周期的周期函数;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,a4=10,且a3、a6、a10成等比数列.
(1)求{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和
,求数列{bn}的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校理科实验班的100名学生期中考试的语文、数学成绩都不低于100分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:[100,110),[110,120),[120,130),[130,140),[140,150].
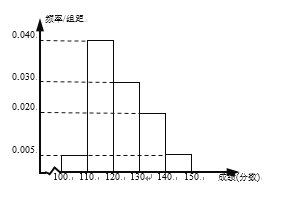
这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 | [100,110) | [110,120) | [120,130) | [130,140) |
| 1:2 | 2:1 | 3:4 | 1:1 |
(1)估计这100名学生语文成绩的平均数、方差(同一组数据用该区间的中点值作代表);
(2)从数学成绩在[130,150] 的学生中随机选取2人,该2人中数学成绩在[140,150]的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将
,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,有下列叫个结论:
的图象,有下列叫个结论:
![]() 在
在![]() 单调递增;
单调递增; ![]() 为奇函数;
为奇函数;
![]() 的图象关于直线
的图象关于直线![]() 对称;
对称; ![]() 在
在![]() 的值域为
的值域为![]() .
.
其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com