
【题目】若| ![]() |=1,|
|=1,| ![]() |=m,|
|=m,| ![]() +
+ ![]() |=2.
|=2.
(1)若| ![]() +2
+2 ![]() |=3,求实数m的值;
|=3,求实数m的值;
(2)若 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为
的夹角为 ![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)证明:因为| ![]() +
+ ![]() |=2,所以|
|=2,所以| ![]() +
+ ![]() |2=4.
|2=4.
即以 ![]() 2+
2+ ![]() 2+2
2+2 ![]()
![]() =4.,
=4.,
又| ![]() |=1,|
|=1,| ![]() |=m,所以
|=m,所以 ![]() .
.
由| ![]() +2
+2 ![]() |=3,所以所以|
|=3,所以所以| ![]() +2
+2 ![]() |2=9.
|2=9.
即以 ![]() 2+4
2+4 ![]() 2+4
2+4 ![]()
![]() =9,
=9,
所以1+4× ![]() +4m2=9,解得m=±1,
+4m2=9,解得m=±1,
又| ![]() |≥0,所以m=1.
|≥0,所以m=1.
(2)证明:因为,| ![]() |=1,|
|=1,| ![]() |=m,
|=m, ![]()
所以| ![]() ﹣
﹣ ![]() |2=
|2= ![]() 2+
2+ ![]() 2﹣2
2﹣2 ![]()
![]() =1﹣2×
=1﹣2× ![]() +m2=2m2﹣2,|
+m2=2m2﹣2,| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
又因为 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为
的夹角为 ![]() ,所以(
,所以( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=以
)=以 ![]() 2﹣
2﹣ ![]() 2=|
2=| ![]() +
+ ![]() |×|
|×| ![]() ﹣
﹣ ![]() |cos
|cos ![]()
即,所以1﹣m2=2× ![]() ,解得m=±
,解得m=± ![]() ,
,
又| ![]() |≥0,所以m=
|≥0,所以m= ![]() .
.
【解析】(1)由| ![]() +
+ ![]() |=2,|
|=2,| ![]() +2
+2 ![]() |=3
|=3 ![]() 2+
2+ ![]() 2+2
2+2 ![]()
![]() =4 和
=4 和 ![]() 2+4
2+4 ![]() 2+4
2+4 ![]()
![]() =9,即可求解;(2)利用(
=9,即可求解;(2)利用( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=以
)=以 ![]() 2﹣
2﹣ ![]() 2=|
2=| ![]() +
+ ![]() |×|
|×| ![]() ﹣
﹣ ![]() |cos
|cos ![]() 求解.
求解.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】分别求出适合下列条件的直线方程: (Ⅰ)经过点P(﹣3,2)且在x轴上的截距等于在y轴上截距的2倍;
(Ⅱ)经过直线2x+7y﹣4=0与7x﹣21y﹣1=0的交点,且和A(﹣3,1),B(5,7)等距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧 ![]() 、
、 ![]() 所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
所在圆的半径分别为f(x)、R米,圆心角为θ(弧度). 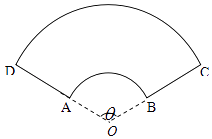
(1)若θ= ![]() ,r1=3,r2=6,求花坛的面积;
,r1=3,r2=6,求花坛的面积;
(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD的长度为多少时,花坛的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC,底面ABC为边长为2 ![]() 的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为AP上一点,AD=2DP,O为底面三角形中心.
的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为AP上一点,AD=2DP,O为底面三角形中心. 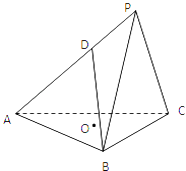
(1)求证DO∥面PBC;
(2)求证:BD⊥AC;
(3)设M为PC中点,求平面MBD和平面BDO所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|f(x)=lg(x﹣1)+ ![]() },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ![]() ,求A∪B;
,求A∪B;
(2)若A∩B=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1 , F2分别是双曲线 ![]() 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在利用“五点法”作函数f(x)=Asin(ωx+)+t(其中A>0, ![]() )的图象时,列出了如表格中的部分数据.
)的图象时,列出了如表格中的部分数据.
x |
|
|
|
|
|
ωx+ | 0 | | π | | 2π |
f(x) | 2 | 6 | 2 | ﹣2 | 2 |
(1)请将表格补充完整,并写出f(x)的解析式.
(2)若 ![]() ,求f(x)的最大值与最小值.
,求f(x)的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x+x2 .
(1)求x<0时,f(x)的解析式;
(2)问是否存在这样的非负数a,b,当x∈[a,b]时,f(x)的值域为[4a﹣2,6b﹣6]?若存在,求出所有的a,b值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com