
【题目】如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
(1)请画出该几何体的三视图;
(2)求四棱锥B﹣CEPD的体积.
【答案】解:(1)该组合体的主视图和侧视图如图示:
(2)∵PD平面ABCD,PD平面PDCE
∴平面PDCE⊥平面ABCD
∵BC⊥CD
∴BC⊥平面PDCE(5分)
∵SPCDE=![]() (PD+EC)DC=3
(PD+EC)DC=3
∴四棱锥B﹣CEPD的体积
V=![]() SPCDEBC=2.
SPCDEBC=2.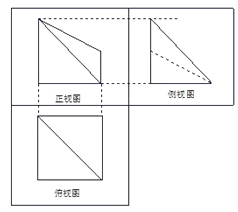
【解析】(1)由已知中底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.根据三视图的定义,易得到该几何体的三视图;
(2)由已知中PD⊥平面ABCD,且PD=AD=2EC=2,我们计算出棱锥的底面面积和高,代入棱体积公式,即可求出四棱锥B﹣CEPD的体积;
【考点精析】本题主要考查了简单空间图形的三视图的相关知识点,需要掌握画三视图的原则:长对齐、高对齐、宽相等才能正确解答此题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
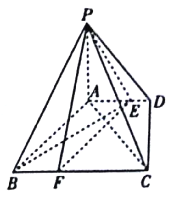
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆Cx2+y2+2x﹣4y+3=0
(1)已知不过原点的直线l与圆C相切,且在x轴,y轴上的截距相等,求直线l的方程;
(2)求经过原点且被圆C截得的线段长为2的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
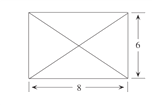
(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第96届(春季)全国糖酒商品交易会于2017年3月23日至25日在四川举办.交易会开始前,展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系,查阅了最近5次交易会的参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下数据:
(袋),得到如下数据:

(Ⅰ)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() 投入使用的每袋原材料相应的销售收入为600元,多余的原材料只能无偿返还.若餐厅原材料现恰好用完,据悉本次交易会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
投入使用的每袋原材料相应的销售收入为600元,多余的原材料只能无偿返还.若餐厅原材料现恰好用完,据悉本次交易会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
(参考公式: 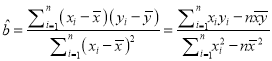 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2mx+m2+4m﹣2.
(1)若函数f(x)在区间[0,1]上是单调递减函数,求实数m的取值范围;
(2)若函数f(x)在区间[0,1]上有最小值﹣3,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,直线
为坐标原点,直线![]() 的方程为
的方程为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点,点
距离最小的点,点![]() 是抛物线上异于点
是抛物线上异于点![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线与抛物线
轴平行的直线与抛物线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求证:直线![]() 恒过定点
恒过定点![]() ;
;
(3)在(2)的条件下过![]() 向
向![]() 轴做垂线,垂足为
轴做垂线,垂足为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )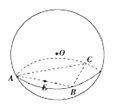
A.![]()
B.2π
C.![]()
D.3π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.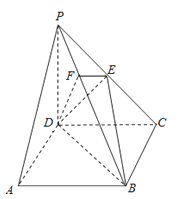
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com