
【题目】已知cosα= ![]() ,cos(α﹣β)=
,cos(α﹣β)= ![]() ,且0<β<α<
,且0<β<α< ![]() ,
,
(1)求tan2α的值;
(2)求β.
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水果树的产量![]() (单位:百千克)与肥料费用(单位:百元)满足如下关系:
(单位:百千克)与肥料费用(单位:百元)满足如下关系:  .此外,还需要投入其它成本(如施肥的人工费等)
.此外,还需要投入其它成本(如施肥的人工费等)![]() 百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为
百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求![]() 的函数关系式;
的函数关系式;
当投入的肥料费用为多少时,该水果树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一组合几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD且PD=AD=2EC=2.
(I)求证:AC⊥平面PDB;
(II)求四棱锥B﹣CEPD的体积;
(III)求该组合体的表面积.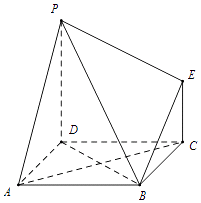
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为y=kx+b(其中k的值与b无关),圆M的方程为x2+y2﹣2x﹣4=0.
(1)如果不论k取何值,直线l与圆M总有两个不同的交点,求b的取值范围;
(2)b=1,l与圆交于A,B两点,求|AB|的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列几个式子,结果为 ![]() 的序号是 ①tan25°+tan35°
的序号是 ①tan25°+tan35° ![]() tan25°tan35°,
tan25°tan35°,
② ![]() ,
,
③2(sin35°cos25°+sin55°cos65°),
④ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上恒不为零的函数,且对任意的x、y∈R都有f(x)f(y)=f(x+y),若a1= ![]() ,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
A.[ ![]() ,1)
,1)
B.[ ![]() ,1]
,1]
C.( ![]() ,1)
,1)
D.( ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6根弹簧进行测量,得到如下数据:
x (g) | 5 | 10 | 15 | 20 | 25 | 30 |
y (cm) | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
(1)画出散点图;
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程. ( 其中 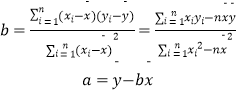 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com