
【题目】设![]() 的倾斜角为
的倾斜角为![]() 绕其上一点
绕其上一点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() 角得到直线
角得到直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() 绕
绕![]() 沿逆时针方向再旋转
沿逆时针方向再旋转![]() 角得到直线
角得到直线![]() ,则
,则![]() 的方程为___________.
的方程为___________.
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() 存在极大值和极小值,且极大值小于极小值,求
存在极大值和极小值,且极大值小于极小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,若线段
,若线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的值;
的值;
(2)已知点![]() 是椭圆
是椭圆![]() 上异于椭圆顶点的一点,延长直线
上异于椭圆顶点的一点,延长直线![]() ,
,![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在区间
在区间![]() 上不是单调函数,求实数
上不是单调函数,求实数![]() 的范围;
的范围;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() ,对任意给定的正实数
,对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() (
(![]() 为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在![]() 轴上?请说明理由.
轴上?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地的出租车价格规定:起步费![]() 元,可行
元,可行![]() 公里,
公里,![]() 公里以后按每公里
公里以后按每公里![]() 元计算,可再行
元计算,可再行![]() 公里;超过
公里;超过![]() 公里按每公里
公里按每公里![]() 元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定。
元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定。
(1)若小明乘出租车从学校到家,共![]() 公里,请问他应付出租车费多少元?
公里,请问他应付出租车费多少元?
(2)求车费![]() (元)与行车里程
(元)与行车里程![]() (公里)之间的函数关系式
(公里)之间的函数关系式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
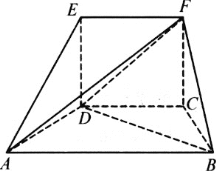
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律.现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com