
【题目】已知函数f(x)=x2﹣x﹣alnx.
(1)当a=3时,求f(x)在[1,2]上的最大值与最小值;
(2)若f(x)在(0,+∞)上单调递增,求a的取值范围.
【答案】(1)![]() ,f(x)max=0(2)
,f(x)max=0(2)![]()
【解析】
(1)首先求出函数的导函数,利用导函数判断函数的单调性,再结合函数的定义域即可求解.
(2)利用导函数转化为f′(x)≥0在(0,+∞)上恒成立,采用分离参数法即a≤2x2﹣x在(0,+∞)上恒成立,令![]() ,求
,求![]() 在
在![]() 的最小值即可.
的最小值即可.
(1)解:当a=3时,f(x)=x2﹣x﹣3lnx(x>0);
![]() ;
;
∴f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
∴当x∈[1,2]时,![]() ;
;
f(1)=0,f(2)=2﹣3ln2;
∴f(x)max=f(1)=0;
(2)解:![]() ;
;
若f(x)在(0,+∞)上单调递增,
即![]() 在(0,+∞)上恒成立;
在(0,+∞)上恒成立;
则a≤2x2﹣x在(0,+∞)上恒成立;
令g(x)=2x2﹣x,则g′(x)=4x﹣1;
易知,![]() ;
;
∴a![]() ,即a的取值范围是
,即a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】设n为正整数,集合A=![]() .对于集合A中的任意元素
.对于集合A中的任意元素![]() 和
和![]() ,记
,记
M(![]() )=
)=![]() .
.
(Ⅰ)当n=3时,若![]() ,
, ![]() ,求M(
,求M(![]() )和M(
)和M(![]() )的值;
)的值;
(Ⅱ)当n=4时,设B是A的子集,且满足:对于B中的任意元素![]() ,当
,当![]() 相同时,M(
相同时,M(![]() )是奇数;当
)是奇数;当![]() 不同时,M(
不同时,M(![]() )是偶数.求集合B中元素个数的最大值;
)是偶数.求集合B中元素个数的最大值;
(Ⅲ)给定不小于2的n,设B是A的子集,且满足:对于B中的任意两个不同的元素![]() ,
,
M(![]() )=0.写出一个集合B,使其元素个数最多,并说明理由.
)=0.写出一个集合B,使其元素个数最多,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x![]() |+|x﹣λ|,其中λ
|+|x﹣λ|,其中λ![]() .
.
(1)若对任意x∈R,恒有f(x)![]() ,求λ的最大值;
,求λ的最大值;
(2)在(1)的条件下,设λ的最大值为t,若正数m,n满足m+2n=mnt,求2m+n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
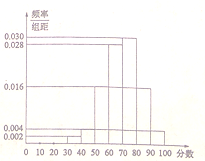
【题目】2016年某市政府出台了“2020年创建全国文明城市(简称创文)”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分, ![]() 内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
(1)求被调查者满意或非常满意该项目的频率;
(2)若从该市的全体市民中随机抽取3人,试估计恰有2人非常满意该项目的概率;
(3)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记![]() 为群众督查员中老年人的人数,求随机变量
为群众督查员中老年人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一个动点M到定点F(3,0)的距离和它到定直线l:x=6的距离之比是常数![]() .
.
(1)求动点M的轨迹T的方程;
(2)若直线l:x+y-3=0与轨迹T交于A,B两点,且线段AB的垂直平分线与T交于C,D两点,试问A,B,C,D是否在同一个圆上?若是,求出该圆的方程;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com