
分析 (Ⅰ)求出导数,利用导数的几何意义,求出a,c,即可求f(x)的解析式;
(Ⅱ)对?x1∈[-3,0],?x2∈[0,+∞)恒有f(x1)≥g(x2)成立,等价于f(x)min≥g(x)max,即可求b的取值范围.
解答 解:(Ⅰ)∵f(x)=x3+ax2-4x+c,
∴f′(x)=3x2+2ax-4,∴f′(1)=2a-1=3,∴a=2
将切点(1,4)代入函数f(x),可得c=5,
∴f(x)=x3+2x2-4x+5;
(Ⅱ)令f′(x)=(x+2)(3x-2)>0,可得x<-2,f′(x)>0,-2<x<0,f′(x)<0,
∵f(-3)=8,f(0)=5,
∴?x1∈[-3,0],f(x)min=f(0)=5,
∵g(x)=lnx+(b-1)x+4,∴g′(x)=$\frac{1}{x}$+b-1,
b-1≥0,b≥1,g′(x)>0,g(x)在(0,+∞)上单调递增,没有最大值,不合题意,舍去;
b-1<0,b<1,令g′(x)=0,x=$\frac{1}{1-b}$,
∴x∈(0,$\frac{1}{1-b}$),g′(x)>0,∴g(x)单调递增,
x∈($\frac{1}{1-b}$,+∞),g′(x)<0,g(x)单调递减,
∴gmax(x)=ln$\frac{1}{1-b}$+3,
∴5≥ln$\frac{1}{1-b}$+3,
∴b≤1-$\frac{1}{{e}^{2}}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查恒成立问题,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
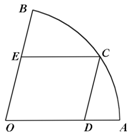 如图,某观光休闲庄园内有一块扇形花卉园OAB,其中O为扇形所在圆的圆心,扇形半径为500米,cos∠AOB=$\frac{1}{4}$.庄园经营者欲在花卉园内修建一条赏花长廊,分别在边OA、弧$\widehat{AB}$、边OB上选点D,C,E修建赏花长廊CD,CE,且CD∥OB,CE∥OA,设CD长为x米,CE长为y米.
如图,某观光休闲庄园内有一块扇形花卉园OAB,其中O为扇形所在圆的圆心,扇形半径为500米,cos∠AOB=$\frac{1}{4}$.庄园经营者欲在花卉园内修建一条赏花长廊,分别在边OA、弧$\widehat{AB}$、边OB上选点D,C,E修建赏花长廊CD,CE,且CD∥OB,CE∥OA,设CD长为x米,CE长为y米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{24}$,0) | B. | ($\frac{5π}{24}$,0) | C. | ($\frac{11π}{24}$,0) | D. | ($\frac{11π}{12}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 15 | C. | 20 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $9\sqrt{2}$ | B. | $\frac{{27\sqrt{2}}}{2}$ | C. | $\frac{{9\sqrt{2}}}{2}$ | D. | $27\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com