
【题目】已知圆![]() :
:![]() ,直线
,直线![]() 过原点
过原点![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)分类讨论:当直线的斜率不存在时,![]() ;当直线
;当直线![]() 的斜率存在时,利用点斜式求出直线方程,再利用点到直线的距离公式使圆心到直线的距离等于半径求出斜率即可.
的斜率存在时,利用点斜式求出直线方程,再利用点到直线的距离公式使圆心到直线的距离等于半径求出斜率即可.
(2)根据题意设直线方程为![]() ,圆心到直线
,圆心到直线![]() 的距离为
的距离为![]() ,利用三角形的面积公式
,利用三角形的面积公式![]() 可得
可得![]() 时
时![]() 的面积最大,从而可得圆心到直线的距离
的面积最大,从而可得圆心到直线的距离![]() ,利用点到直线的距离公式即可求解.
,利用点到直线的距离公式即可求解.
(1)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
此时直线![]() 与圆
与圆![]() 相切,
相切,
∴![]() 符合题意:
符合题意:
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的斜率为
的斜率为![]() ,
,
则直线![]() 方程为
方程为![]() ,即
,即![]() .
.
则![]() ,解得
,解得![]() ,
,
即直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)∵直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,∴直线
两点,∴直线![]() 的斜率存在,
的斜率存在,
设直线方程为![]() ,圆心到直线
,圆心到直线![]() 的距离为
的距离为![]() ,
,
由于![]() ,
,
∴当![]() 取最大值1,即
取最大值1,即![]() 时
时![]() 的面积最大.
的面积最大.
此时![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() .
.
故直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱![]() 中,侧棱
中,侧棱![]() 垂直底面,∠ACB=90°,
垂直底面,∠ACB=90°,![]() ,D为
,D为![]() 的中点,点P为AB的中点.
的中点,点P为AB的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥B-CDP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数![]() ,
,![]() ,是否存在实数m,使得
,是否存在实数m,使得![]() 的最小值为2,若存在,请求出m的值;若不存在,请说明理由.
的最小值为2,若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
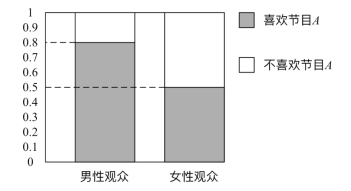
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: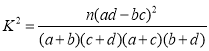
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手车直卖网站对其所经营的一款品牌汽车的使用年数x与销售价格y(单位:万元,辆)进行了记录整理,得到如下数据:

(I)画散点图可以看出,z与x有很强的线性相关关系,请求出z与x的线性回归方程(回归系数![]() 精确到0.01);
精确到0.01);
(II)求y关于x的回归方程,并预测某辆该款汽车当使用年数为10年时售价约为多少.
参考公式:
参考数据:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产某种产品,为了提高生产效益,通过引进先进的生产技术和管理方式进行改革,并对改革后该产品的产量x(万件)与原材料消耗量y(吨)及100件产品中合格品与不合格品数量作了记录,以便和改革前作对照分析,以下是记录的数据:
表一:改革后产品的产量和相应的原材料消耗量
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
表二:改革前后定期抽查产品的合格数与不合格数
合格品的数量 | 不合格品的数量 | 合计 | |
改革前 | 90 | 10 | 100 |
改革后 | 85 | 15 | 100 |
合计 | 175 | 25 | 200 |
(1)请根据表一提供数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(2)已知改革前生产7万件产品需要6.5吨原材料,根据回归方程预测生产7万件产品能够节省多少原材料?
(3)请根据表二提供的数据,判断是否有90%的把握认为“改革前后生产的产品的合格率有差异”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com