
分析 建立直角坐标系,设P点坐标,列方程,化简,求出P的轨迹方程,(S1+S2)2=$\frac{1}{4}$(PM+PN)2=$\frac{2+\sqrt{3}}{2}$PN2,求出PO22的最大值,即可得出结论.
解答 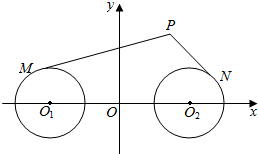 解:由题意,O1(-2,0),O2(2,0),
解:由题意,O1(-2,0),O2(2,0),
由已知PM=$\sqrt{3}$PN,得PM2=3PN2.
因为两圆的半径均为1,所以PO12-1=3(PO22-1).
设P(x,y),则(x+2)2+y2-1=3[(x-2)2+y2-1],
即(x-4)2+y2=13,
(S1+S2)2=$\frac{1}{4}$(PM+PN)2=$\frac{2+\sqrt{3}}{2}$PN2,
求出PO22的最大值,即可得出结论.
∵PO2的最大值为2+$\sqrt{13}$,
∴PO22的最大值为17+4$\sqrt{13}$,
∴PN2的最大值16+4$\sqrt{13}$,
∴(S1+S2)2的最大值为$\frac{2+\sqrt{3}}{2}$×(16+4$\sqrt{13}$)=16+4$\sqrt{13}$+8$\sqrt{3}$+2$\sqrt{39}$.
故答案为:16+4$\sqrt{13}$+8$\sqrt{3}$+2$\sqrt{39}$.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查面积的计算,确定P的轨迹方程是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
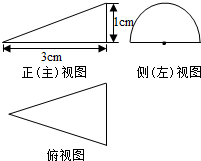 一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )
一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )| A. | $\frac{(\sqrt{10}+1)π}{2}$cm2 | B. | ($\frac{(\sqrt{10}+1)π}{2}$+3)cm2 | C. | ($\frac{π}{2}$+3)cm2 | D. | ($\frac{\sqrt{10}π}{2}$+3)cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com