若函数f(x)=x3-3x+m在[0,2]上存在两个不同的零点,则实数m的取值范围是________.
0≤m<2
分析:利用导数求出函数f(x)的单调区间及极大值、极小值、f(0)、f(2),由函数f(x)=x
3-3x+m在[0,2]上存在两个不同零点,可对f(0)、f(1)、f(2)的符号进行限制,由此可求出m的取值范围.
解答:f′(x)=3x
2-3=3(x+1)(x-1),
当x<-1或x>1时,f′(x)>0,当-1<x<1时,f′(x)<0,
所以f(x)在(-∞,-1),(1,+∞)上单调递增;在(-1,1)上单调递减.
所以当x=-1时f(x)取得极大值f(-1)=2+m,当x=1时f(x)取得极小值f(1)=-2+m,f(0)=m,f(2)=2+m.
因为函数f(x)=x
3-3x+m在[0,2]上存在两个不同的零点,
所以
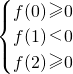
,即
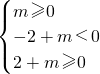
,解得0≤m<2.
故答案为:0≤m<2.
点评:本题考查应用导数研究函数的单调性、极值问题,考查分析问题解决问题的能力以及数形结合思想的应用.

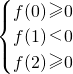 ,即
,即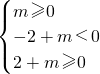 ,解得0≤m<2.
,解得0≤m<2.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案