
【题目】已知数列{an}和{bn}满足a1a2a3…an= ![]() (n∈N*).若{an}为等比数列,且a1=2,b3=6+b2 .
(n∈N*).若{an}为等比数列,且a1=2,b3=6+b2 .
(1)求an和bn;
(2)设cn= ![]() (n∈N*).记数列{cn}的前n项和为Sn .
(n∈N*).记数列{cn}的前n项和为Sn .
(i)求Sn;
(ii)求正整数k,使得对任意n∈N*均有Sk≥Sn .
【答案】
(1)解:∵a1a2a3…an= ![]() (n∈N*) ①,
(n∈N*) ①,
当n≥2,n∈N*时, ![]() ②,
②,
由①②知: ![]() ,
,
令n=3,则有 ![]() .
.
∵b3=6+b2,
∴a3=8.
∵{an}为等比数列,且a1=2,
∴{an}的公比为q,则 ![]() =4,
=4,
由题意知an>0,∴q>0,∴q=2.
∴ ![]() (n∈N*).
(n∈N*).
又由a1a2a3…an= ![]() (n∈N*)得:
(n∈N*)得:
![]() ,
,
![]() ,
,
∴bn=n(n+1)(n∈N*).
(2)解:(i)∵cn= ![]() =
= ![]() =
= ![]() .
.
∴Sn=c1+c2+c3+…+cn
= ![]()
= ![]()
= ![]()
= ![]() ;
;
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
![]() ,
,
而
![]() =
= ![]() >0,
>0,
得
![]() ,
,
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有S4≥Sn,故k=4
【解析】(1)先利用前n项积与前(n﹣1)项积的关系,得到等比数列{an}的第三项的值,结合首项的值,求出通项an , 然后现利用条件求出通项bn;(2)(i)利用数列特征进行分组求和,一组用等比数列求和公式,另一组用裂项法求和,得出本小题结论;(ii)本小题可以采用猜想的方法,得到结论,再加以证明.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知圆C的圆心C在直线![]() 上.
上.
![]() 若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为
若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为![]() ,求圆C的标准方程;
,求圆C的标准方程;
![]() 已知点
已知点![]() ,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使
,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使![]() 为坐标原点
为坐标原点![]() ,求圆心C的纵坐标的取值范围.
,求圆心C的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 和
和![]() 满足:
满足:![]() 在区间
在区间![]() 上均有定义;
上均有定义;![]() 函数
函数![]() 在区间
在区间![]() 上至少有一个零点,则称
上至少有一个零点,则称![]() 和
和![]() 在
在![]() 上具有关系W.
上具有关系W.
![]() 若
若![]() ,
,![]() ,判断
,判断![]() 和
和![]() 在
在![]() 上是否具有关系W,并说明理由;
上是否具有关系W,并说明理由;
![]() 若
若![]() 和
和![]() 在
在![]() 上具有关系W,求实数m的取值范围.
上具有关系W,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位: ![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示一天内抽取的16个零件中其尺寸在
表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及
及![]() 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得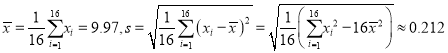 ,其中
,其中![]() 为
为
抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
①BD平分∠CBF;
②FB2=FDFA;
③AECE=BEDE;
④AFBD=ABBF.
所有正确结论的序号是( )
A.①②
B.③④
C.①②③
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β. 
(1)设计中CD是铅垂方向,若要求α≥2β,问CD的长至多为多少(结果精确到0.01米)?
(2)施工完成后,CD与铅垂方向有偏差,现在实测得α=38.12°,β=18.45°,求CD的长(结果精确到0.01米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com