
【题目】设![]() ,
, ![]() 满足约束条件
满足约束条件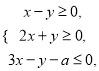 若目标函数
若目标函数![]() 的最小值为
的最小值为![]() ,则实数
,则实数![]() 的值为
的值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题有__________.
①回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数![]() 来刻画回归效果,
来刻画回归效果, ![]() 越接近
越接近![]() ,说明模型的拟合效果越好;
,说明模型的拟合效果越好;
④用系统抽样法从![]() 名学生中抽取容量为
名学生中抽取容量为![]() 的样本,将
的样本,将![]() 名学生从
名学生从![]() 编号,按编号顺序平均分成
编号,按编号顺序平均分成![]() 组(
组(![]() 号,
号, ![]() 号,
号, ![]() 号),若第
号),若第![]() 组抽出的号码为
组抽出的号码为![]() ,则第一组中用抽签法确定的号码为
,则第一组中用抽签法确定的号码为![]() 号.
号.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
t |
|
|
|
|
|
|
男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)﹣x2 , 在(1,2)内任取两个实数x1 , x2(x1≠x2),若不等式 ![]() >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )
A.(28,+∞)
B.[15,+∞)
C.[28,+∞)
D.(15,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二八班选出甲、乙、丙三名同学参加级部组织的科学知识竞赛.在该次竞赛中只设成绩优秀和成绩良好两个等次,若某同学成绩优秀,则给予班级10分的班级积分,若成绩良好,则给予班级5分的班级积分.假设甲、乙、丙成绩为优秀的概率分别为 ![]() ,
, ![]() ,
, ![]() ,他们的竞赛成绩相互独立.
,他们的竞赛成绩相互独立.
(1)求在该次竞赛中甲、乙、丙三名同学中至少有一名成绩为优秀的概率;
(2)记在该次竞赛中甲、乙、丙三名同学所得的班级积分之和为随机变量ξ,求随机变量ξ的分布列和数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com