
【题目】已知动点P到定点![]() 的距离与点P到定直线
的距离与点P到定直线![]() 的距离之比为
的距离之比为![]()
(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E是点F关于原点的对称点,若![]() ,求 | MN | 的最小值.
,求 | MN | 的最小值.
【答案】(1)![]() = 1(2)2
= 1(2)2![]()
【解析】
(1)用坐标表示条件,化简即得轨迹方程(2)先设坐标,再用坐标表示| MN |,根据条件![]() 得坐标关系,代入| MN |表达式,最后根据基本不等式求最值
得坐标关系,代入| MN |表达式,最后根据基本不等式求最值
(1)设点P(x,y)
依题意,有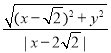 =
=![]()
整理得:![]() = 1
= 1
所以动点P的轨迹方程为![]() = 1
= 1
(2)∵点E与点F关于原点对称
∴E(-![]() ,0)
,0)
∵M、N是l上的两点
∴可设M(2![]() ,y1) N(2
,y1) N(2![]() ,y2)
,y2)
(不妨设,y1>y2)
∵![]()
∴(3![]() ,y1)·(
,y1)·(![]() ,y2)=0
,y2)=0
即6 + y1y2=0
∴y2=-![]()
由于y1>y2,∴y1>0,y2<0
∴| MN |=y1-y2=y1+![]() ≥2
≥2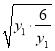 =2
=2![]()
当且仅当y1=![]() ,y2=-
,y2=-![]() 时,取“=”号,故| MN |的最小值为2
时,取“=”号,故| MN |的最小值为2![]()


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】朱载堉(1536~1611),是中国明代一位杰出的音乐家、数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度13个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为![]() ,第七个音的频率为
,第七个音的频率为![]() ,则
,则![]() =
=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
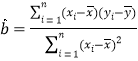
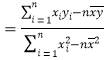 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作为交通重要参与者的行人,闯红灯通行频有发生,带来了较大的交通安全隐患.在某十字路口,交警部门从穿越该路口的行人中随机抽取了200人进行调查,得到不完整的![]() 列联表如图所示:
列联表如图所示:
年龄低于30岁 | 年龄不低于30岁 | 合计 | |
闯红灯 | 60 | 80 | |
未闯红灯 | 80 | ||
合计 | 200 |
(1)将![]() 列联表补充完整;
列联表补充完整;
(2)是否有99.9%的把握认为行人是否闯红灯与年龄有关.
参考公式及数据: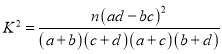 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
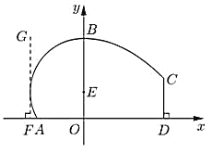
【题目】某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]()
![]() ,
,![]() 是圆的切线,且
是圆的切线,且![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]()
![]() 的一部分,
的一部分,![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.
的半径.
(1)若![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)若体育馆侧面的最大宽度![]() 不超过75米,求
不超过75米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为
所表示的曲线为![]() ,则有以下几个命题:
,则有以下几个命题:
①当![]() 时,曲线
时,曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;
轴上的椭圆;
②当![]() 时,曲线
时,曲线![]() 表示双曲线;
表示双曲线;
③当![]() 时,曲线
时,曲线![]() 表示圆;
表示圆;
④存在![]() ,使得曲线
,使得曲线![]() 为等轴双曲线 .
为等轴双曲线 .
以上命题中正确的命题的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com