
【题目】为了解某班学生喜欢数学是否与性别有关,对本班![]() 人进行了问卷调查得到了如下的列联表,已知在全部
人进行了问卷调查得到了如下的列联表,已知在全部![]() 人中随机抽取
人中随机抽取![]() 人抽到喜欢数学的学生的概率为
人抽到喜欢数学的学生的概率为![]() .
.
喜欢数学 | 不喜欢数学 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过![]() 的前提下认为喜欢数学与性别有关?说明你的理由;
的前提下认为喜欢数学与性别有关?说明你的理由;
(3)现从女生中抽取![]() 人进一步调查,设其中喜欢数学的女生人数为
人进一步调查,设其中喜欢数学的女生人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
下面的临界表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: ,其中
,其中![]() )
)
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】山东省于2015年设立了水下考古研究中心,以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站,分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解,然后再选择合适的时机下水探摸、打捞,省水下考古中心在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业,其用氧量包含以下三个方面:
米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.4升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升.
米/分钟,每分钟用氧量为0.32升.
潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(Ⅰ)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是抛物线C:![]() 上任意一点,过点P作直线PH⊥x轴,点H为垂足.点M是直线PH上一点,且在抛物线的内部,直线l过点M交抛物线C于A、B两点,且点M是线段AB的中点.
上任意一点,过点P作直线PH⊥x轴,点H为垂足.点M是直线PH上一点,且在抛物线的内部,直线l过点M交抛物线C于A、B两点,且点M是线段AB的中点.
(1)证明:直线l平行于抛物线C在点P处切线;
(2)若|PM|=![]() , 当点P在抛物线C上运动时,△PAB的面积如何变化?
, 当点P在抛物线C上运动时,△PAB的面积如何变化?
查看答案和解析>>
科目:高中数学 来源: 题型:
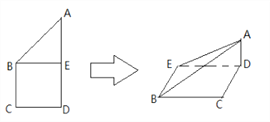
【题目】如图所示,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:①
点,则翻折后的几何体中有如下描述:①![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正确的命题序号为___________.
,其中正确的命题序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底部ABCD为菱形,E为CD的中点.
平面ABCD,底部ABCD为菱形,E为CD的中点.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱台![]() 中,点
中,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 内(含边界)的一个动点,且有平面
内(含边界)的一个动点,且有平面![]() 平面
平面![]() ,则动点
,则动点![]() 的轨迹是( )
的轨迹是( )

A. 平面B. 直线C. 线段,但只含1个端点D. 圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,
两点,![]() 的最大值是
的最大值是![]() ,
,![]() 的最小值是
的最小值是![]() ,且满足
,且满足![]() .
.
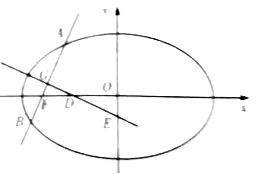
(1)求椭圆的离心率;
(2)设线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点,记
是坐标原点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆台的上、下底面半径分别为![]() 、
、![]() ,母线长
,母线长![]() ,从圆台母线
,从圆台母线![]() 的中点
的中点![]() 拉一条绳子绕圆台侧面转到
拉一条绳子绕圆台侧面转到![]() 点(
点(![]() 在下底面),求:
在下底面),求:
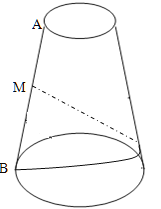
(1)绳子的最短长度;
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车从![]() 市出发沿海岸一条笔直公路以每小时
市出发沿海岸一条笔直公路以每小时![]() 的速度向东均速行驶,汽车开动时,在
的速度向东均速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com