
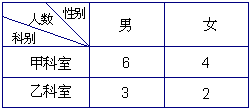
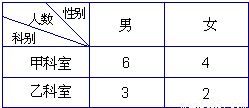
 某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.
某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.| 3 |
| 15 |
| 3 |
| 15 |
| ||
|
| 2 |
| 3 |
| ||
|
| ||
|
| 4 |
| 75 |
| ||||
|
| ||
|
| ||
|
| ||
|
| 22 |
| 75 |
| ||
|
| ||
|
| 1 |
| 5 |
| 34 |
| 75 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 4 |
| 75 |
| 22 |
| 75 |
| 34 |
| 75 |
| 1 |
| 5 |
| 9 |
| 5 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
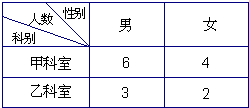 某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.
某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
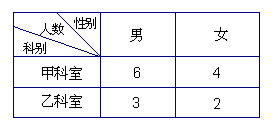
某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.
(1)求从甲、乙两科室各抽取的人数;
(2)求从甲科室抽取的工作人员中至少有1名女性的概率;
(3)记![]() 表示抽取的3名工作人员中男性的人数,求
表示抽取的3名工作人员中男性的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省河源市龙川一中高三(上)8月月考数学试卷(理科)(解析版) 题型:解答题
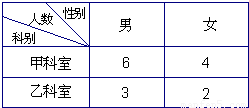
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市启恩中学高三数学综合训练7(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com