
【题目】如图,在正方体ABCD﹣A1B1C1D1中,棱长为a,E是棱DD1的中点 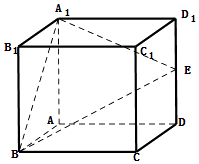
(1)求三棱锥E﹣A1B1B的体积;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
【答案】
(1)解: ![]()
(2)解:存在.
取C1D1中点F,连B1F,EF,C1D,连B1A交A1B于O,
∵EF是△D1C1D的中位线∴ ![]() ,
,
因为正方体ABCD﹣A1B1C1D1
所以 ![]()
又因为四边形B1ADC1是平行四边形,
所以B1A∥C1D,B1A=C1D
所以B1O∥EF,B1O=EF,
所以四边形B1OEF是平行四边形,
所以B1F∥OE,
所以B1F∥平面A1BE.
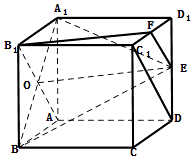
【解析】(1)代入棱锥的体积公式计算;(2)取C1D1中点F,连B1F,EF,C1D,连B1A交A1B于O,则可证四边形B1OEF为平行四边形,得出BF∥OE,从而得出B1F∥平面A1BE.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin ωxcos ωx-sin2ωx+1(ω>0)图象的相邻两条对称轴之间的距离为
sin ωxcos ωx-sin2ωx+1(ω>0)图象的相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求ω的值及函数f(x)的单调递减区间;
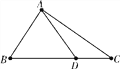
(Ⅱ)如图,在锐角三角形ABC中有f(B)=1,若在线段BC上存在一点D使得AD=2,且AC=![]() ,CD=
,CD=![]() -1,求三角形ABC的面积.
-1,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)设全集为R,A={x|3<x<7},B={x|4<x<10},求R(A∪B)及(RA)∩B.
(2)C={x|a﹣4≤x≤a+4},且A∩C=A,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且离心率为
,且离心率为![]() ,点
,点![]() 为椭圆上一动点,
为椭圆上一动点, ![]() 内切圆面积的最大值为
内切圆面积的最大值为![]() .
.
(1)求椭圆的方程;
(2)设椭圆的左顶点为![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,连接
两点,连接![]() 并延长分别交直线
并延长分别交直线![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否恒过定点?若是,请求出定点坐标;若不是,请说明理由.
为直径的圆是否恒过定点?若是,请求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km). 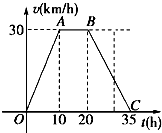
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(x2﹣3)ex , 当m在R上变化时,设关于x的方程f2(x)﹣mf(x)﹣ ![]() =0的不同实数解的个数为n,则n的所有可能的值为( )
=0的不同实数解的个数为n,则n的所有可能的值为( )
A.3
B.1或3
C.3或5
D.1或3或5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com