
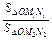 =
=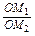 ·
·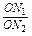 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.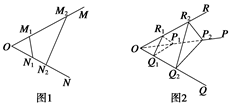
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:解答题
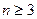 ,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数
,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数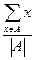 与
与 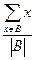
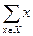 与
与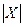 分别表示有限数集
分别表示有限数集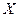 的所有元素之和及元素个数.)
的所有元素之和及元素个数.)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.使用了归纳推理 | B.使用了类比推理 |
| C.使用了“三段论”,但大前提错误 | D.使用了“三段论”,但小前提错误 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
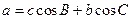 ;类比上述结论,写出下列条件下的结论:四面体P-ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是
;类比上述结论,写出下列条件下的结论:四面体P-ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是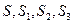 ,二面角
,二面角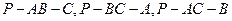 的度数分别是
的度数分别是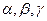 ,则
,则 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com