
【题目】在△ABC中,角A,B,C的对边分别为a,b,c, 且![]() , 若
, 若![]() .
.
(1)求角B的大小;
(2)若![]() , 且△ABC的面积为
, 且△ABC的面积为![]() , 求sinA的值.
, 求sinA的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由正弦定理,同角三角函数基本关系式化简已知,结合sinA≠0,sinB≠0,可求cosB![]() ,结合范围0<B<π,可得B的值;
,结合范围0<B<π,可得B的值;
(2)由已知利用三角形的面积公式可求ac的值,由余弦定理得a+c=4,联立解得a,c的值,由正弦定理即可解得sinA的值.
(1)在ABC中,sin(B+C) = sinA , 由正弦定理和已知条件得:
sinAtanB = 2sinBsinA , 由于sinA 0 , sinB 0, 则有:cosB =![]() , 又0<B< ,
, 又0<B< ,
所以B =![]()
(2)由题可知:SABC = ![]() acsinB =
acsinB = ![]() acsin
acsin![]() =
=![]() , ac=3 ,
, ac=3 ,
在ABC中由余弦定理得:b2=a2+c2-2accos![]() , 即有:7= a2+c2- ac , 整理得:
, 即有:7= a2+c2- ac , 整理得:
(a+c)2 - 3ac = 7 , 代入得:(a+c)2 =16 , a + c = 4 ,
解方程组![]() , 又a>c,得:a=3,c=1 , 由正弦定理得:
, 又a>c,得:a=3,c=1 , 由正弦定理得:![]() ,
,
sinA = ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】![]() 是双曲线
是双曲线![]() 上一点,
上一点, ![]() 分别是双曲线
分别是双曲线![]() 的左、右顶点,直线
的左、右顶点,直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求双曲线的离心率;
(2)过双曲线![]() 的右焦点且斜率为
的右焦点且斜率为![]() 的直线交双曲线于
的直线交双曲线于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() 为双曲线上一点,满足
为双曲线上一点,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】即将于![]() 年夏季毕业的某大学生准备到贵州非私营单位求职,为了了解工资待遇情况,他在贵州省统计局的官网上,查询到
年夏季毕业的某大学生准备到贵州非私营单位求职,为了了解工资待遇情况,他在贵州省统计局的官网上,查询到![]() 年到
年到![]() 年非私营单位在岗职工的年平均工资近似值(单位:万元),如下表:
年非私营单位在岗职工的年平均工资近似值(单位:万元),如下表:
年份 |
|
|
|
|
|
|
|
|
|
|
序号 |
|
|
|
|
|
|
|
|
|
|
年平均工资 |
|
|
|
|
|
|
|
|
|
|
(1)请根据上表的数据,利用线性回归模型拟合思想,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 的计算结果根据四舍五入精确到小数点后第二位);
的计算结果根据四舍五入精确到小数点后第二位);
(2)如果毕业生对年平均工资的期望值为8.5万元,请利用(1)的结论,预测![]() 年的非私营单位在岗职工的年平均工资(单位:万元。计算结果根据四舍五入精确到小数点后第二位),并判断
年的非私营单位在岗职工的年平均工资(单位:万元。计算结果根据四舍五入精确到小数点后第二位),并判断![]() 年平均工资能否达到他的期望.
年平均工资能否达到他的期望.
参考数据:![]() ,
,![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附:对于一组具有线性相关的数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为

 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 为椭圆的左、右焦点,点
为椭圆的左、右焦点,点![]() 在直线
在直线![]() 上且不在
上且不在![]() 轴上,直线
轴上,直线![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() ,
,![]() 为坐标原点.
为坐标原点.
![]() 设直线
设直线![]() 的斜率为
的斜率为![]() ,证明:
,证明:![]()
![]() 问直线
问直线![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 的斜率
的斜率![]() 满足
满足![]() ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月1日,贵阳市地铁一号线全线开通,在一定程度上缓解了出行的拥堵状况.为了了解市民对地铁一号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图:
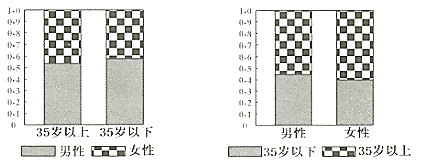
根据图中(![]() 岁以上含
岁以上含![]() 岁)的信息,下列结论中不一定正确的是( )
岁)的信息,下列结论中不一定正确的是( )
A. 样本中男性比女性更关注地铁一号线全线开通
B. 样本中多数女性是![]() 岁以上
岁以上
C. ![]() 岁以下的男性人数比
岁以下的男性人数比![]() 岁以上的女性人数多
岁以上的女性人数多
D. 样本中![]() 岁以上的人对地铁一号线的开通关注度更高
岁以上的人对地铁一号线的开通关注度更高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com