
已知函数f(x)=2sin ωx·cos ωx+2 cos2ωx-
cos2ωx- (其中ω>0),且函数f(x)的周期为π.
(其中ω>0),且函数f(x)的周期为π.
(1)求ω的值;
(2)将函数y=f(x)的图象向右平移 个单位长度,再将所得图象各点的横坐标缩小到原来的
个单位长度,再将所得图象各点的横坐标缩小到原来的 倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在
倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在 上的单调区间.
上的单调区间.
(1)ω=1(2)单调递增区间为 ,单调递减区间为
,单调递减区间为
【解析】(1)因为f(x)=2sin ωx·cos ωx+2 cos2ωx-
cos2ωx- =sin 2ωx+
=sin 2ωx+ cos 2ωx=2sin
cos 2ωx=2sin  ,
,
又因为函数f(x)的周期为π,且ω>0,所以T= =
= =π,所以ω=1.
=π,所以ω=1.
(2)由(1)知,f(x)=2sin 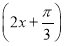 .
.
将函数y=f(x)的图象向右平移 个单位后得到函数y=2sin2
个单位后得到函数y=2sin2  +
+ =2sin
=2sin  的图象,再将所得图象各点的横坐标缩小为原来的
的图象,再将所得图象各点的横坐标缩小为原来的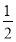 倍(纵坐标不变),得到函数g(x)=2sin(4x-
倍(纵坐标不变),得到函数g(x)=2sin(4x- )的图象.
)的图象.
由- +2kπ≤4x-
+2kπ≤4x- ≤
≤ +2kπ(k∈Z),
+2kπ(k∈Z),
得 -
-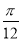 ≤x≤
≤x≤ +
+ (k∈Z);
(k∈Z);
由 +2kπ≤4x-
+2kπ≤4x-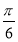 ≤
≤ +2kπ(k∈Z),
+2kπ(k∈Z),
得 +
+ ≤x≤
≤x≤ +
+ (k∈Z).
(k∈Z).
故函数g(x)在 上的单调递增区间为
上的单调递增区间为 ,单调递减区间为
,单调递减区间为


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:选择题
如图,某几何体的正视图、侧视图、俯视图均为直角三角形,则这个几何体的表面中,直角三角形个数为( ).

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:填空题
一出租车司机从饭店到火车站的途中经过六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3 cm,4 cm,以AC为直径的圆与AB交于点D,则BD=________cm.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
如图,已知PA,PB是圆O的切线,A,B分别为切点,C为圆O上不与A,B重合的另一点,若∠ACB=120°,则∠APB=________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:选择题
已知函数f(x)=sin (2x+φ),其中φ为实数,若f(x)≤ 对x∈R恒成立,且
对x∈R恒成立,且 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).
A. =-1
=-1
B.f >f
>f
C.f(x)是奇函数
D.f(x)的单调递增区间是 (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:解答题
设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}.
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I长度的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:选择题
已知函数y=f(x)(x∈R)的图象如图所示,则不等式xf′(x)<0的解集为( ).

A.  ∪
∪ B.
B. 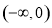 ∪
∪
C.  ∪
∪ D.
D. 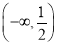 ∪
∪
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:选择题
甲射击命中目标的概率是 ,乙命中目标的概率是
,乙命中目标的概率是 ,丙命中目标的概率是
,丙命中目标的概率是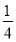 .现在三人同时射击目标,则目标被击中的概率为( ).
.现在三人同时射击目标,则目标被击中的概率为( ).
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com