
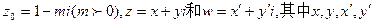 均为实数,
均为实数,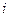 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数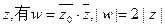 。
。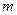 的值,并分别写出
的值,并分别写出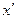 和
和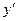 用
用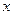 、
、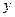 表示的关系式;
表示的关系式;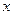 、
、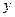 )作为点
)作为点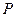 的坐标,(
的坐标,(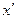 、
、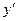 )作为点
)作为点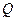 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点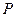 变到这一平面上的点
变到这一平面上的点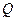 ,
,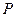 在直线
在直线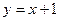 上移动时,试求点
上移动时,试求点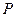 经该变换后得到的点
经该变换后得到的点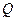 的轨迹方程;
的轨迹方程; 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com