
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | [1,+∞) |
分析 分别令g(x)=lnx-x2+x,h(x)=a(x+1),x∈(0,+∞),利用导数判出函数g(x)在(0,+∞)上的单调性并求其最大值,结合两个函数的图象的大致形状即可求得a的范围.
解答 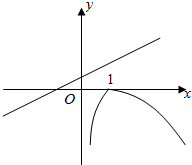 解:令g(x)=lnx-x2+x,h(x)=a(x+1),x∈(0,+∞),
解:令g(x)=lnx-x2+x,h(x)=a(x+1),x∈(0,+∞),
则$g′(x)=\frac{1}{x}-2x+1=\frac{-2{x}^{2}+x+1}{x}$=$-\frac{(2x+1)(x-1)}{x}$,
∴当x>1时,g′(x)<0,g(x)单调递减;
当0<x<1时,g′(x)>0,g(x)单调递增.
∴g(x)max=g(1)=0.
h(x)表示过定点(-1,0)的直线在x∈(0,+∞)的部分,
作出两个函数的简图如图:
由图象可得:a>0.
故选:A.
点评 本题考查函数恒成立问题,考查数学转化思想方法,数形结合使问题更加直观,是中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 0 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 2014年某大学自主招生面试环节中,七位评委为一考生打出分数的茎叶图如图21,去掉一个最高分和一个最低分,所剩数据的平均数,众数和中位数分别为( )
2014年某大学自主招生面试环节中,七位评委为一考生打出分数的茎叶图如图21,去掉一个最高分和一个最低分,所剩数据的平均数,众数和中位数分别为( )| A. | 84,84,86 | B. | 84,84,84 | C. | 85,84,86 | D. | 85,84,84 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com