
����Ŀ������ʵʩ�����ſ����ߺ�Ϊ���˽����ǶԴ����߳�֧��̬���Ƿ��������йأ��������Ž��ѻ�������һ���ľ���ֳ��������飨45�����ϣ���45�꣩���������飨45�����£�����45�꣩�������ÿ������������50�ˣ��Ը����г�֧��̬�ȺͲ�֧��̬�ȵ�����ռ��Ƶ�ʻ��Ƴɵȸ�����ͼ����ͼ��ʾ�� 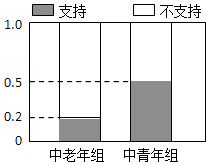
֧�� | ��֧�� | �ϼ� | |
�������� | 50 | ||
�������� | 50 | ||
�� �� | 100 |
��1������������Ϣ���2��2��������
��2���Ƿ���99%���ϵİ�����Ϊ���ǶԴ����߳�֧��̬���������йأ�
P��K2��k0�� | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
���� ![]() ��
��
���𰸡�
��1���⣺�ɵȸ�����ͼ��֪��
���������У���֧��̬�ȵ���50��0.2=10�ˣ��ֲ�֧��̬�ȵ���50��10=40�ˣ�
���������У���֧��̬�ȵ���50��0.5=25�ˣ��ֲ�֧��̬�ȵ���50��25=25�ˣ�
��2��2��������
֧�� | ��֧�� | �ϼ� | |
�������� | 10 | 40 | 50 |
�������� | 25 | 25 | 50 |
�� �� | 35 | 65 | 100 |
��2���⣺ ![]() ��
��
����99%���ϵİ�����Ϊ���ǶԴ����߳�֧��̬��֧���������й�
����������1�����ݵȸ�����ͼ�������������ÿһ������������2��2���������ɣ���2������2��2����������K2��ֵ���Ӷ��жϽ��ۼ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
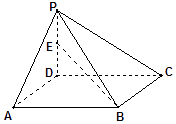
����Ŀ����ͼ��������P��ABCD�У�����ABCD�������Σ�EΪPD�е㣬�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ����
���� ![]() =�� ��
=�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У���С������Ϊ����Ϊ�溯�����ǣ� ��
A.y=sin ![]()
B.y=cos ![]()
C.y=cos2x
D.y=sin2x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ��ǡ�ABC�Ľ�A��B��C���Եıߣ���c=2��C= ![]() ��
��
��1������ABC��������� ![]() ����a��b��
����a��b��
��2����sinC+sin��B��A��=2sin2A����A��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A��0��3����ֱ��l��y=2x��4����ԲC�İ뾶Ϊ1��Բ����l�ϣ� 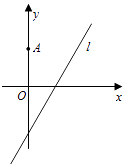
��1����Բ��CҲ��ֱ��y=x��1�ϣ�����A��ԲC�����ߣ������ߵķ��̣�
��2����ԲC�ϴ��ڵ�M��ʹMA=2MO����Բ��C�ĺ�����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�߶��꼶��һ����ѧ����������ȡ�˲���ѧ������ѧ�ɼ����һ���������õ�����Ƶ�ʷֲ�ֱ��ͼ�� 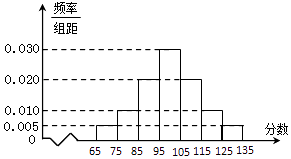
��1�����ⲿ��ѧ���ɼ�������ƽ���� ![]() ����������s2��ͬһ�������ø�����е�ֵ��Ϊ������
����������s2��ͬһ�������ø�����е�ֵ��Ϊ������
��2����Ƶ�ʷֲ�ֱ��ͼ������Ϊ����У�߶�ѧ������β����е���ѧ�ɼ�X������̬�ֲ� ![]() �� ��������̬�ֲ�����P��X��129����
�� ��������̬�ֲ�����P��X��129����
������У�߶�����1000��ѧ���������âٵĽ��������β����У���ѧ�ɼ���129�����ϣ���129�֣���ѧ���������������������ʾ��
������ ![]() ��14.5����X��N���̣���2������P���̩�2�ң�X����+2�ң�=0.9544��
��14.5����X��N���̣���2������P���̩�2�ң�X����+2�ң�=0.9544��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪p������ ![]() =1��ʾ������x���ϵ���Բ��q��˫����
=1��ʾ������x���ϵ���Բ��q��˫���� ![]() =1��������e�ʣ�
=1��������e�ʣ� ![]() ��
�� ![]() ����
����
��1������Բ ![]() =1�Ľ����˫����
=1�Ľ����˫���� ![]() =1�Ķ����غϣ���ʵ��m��ֵ��
=1�Ķ����غϣ���ʵ��m��ֵ��
��2������p��q���������⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������E��1��0����ֱ����ԲO��x2+y2=4�ཻ��A��B���㣬����C��2��0������AB��ֱ��ֱ����ԲO����һ����ΪD�� 
��1������B����Ϊ��0����2��ʱ����ֱ��CD�ķ��̣�
��2�����ı���ABCD���S�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com