
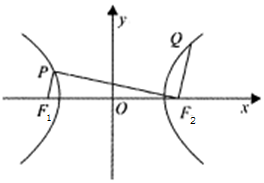
 设F1,F2为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,P,Q分别为双曲线左、右支上的点,若$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,则双曲线的离心率为( )
设F1,F2为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,P,Q分别为双曲线左、右支上的点,若$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,则双曲线的离心率为( )| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
分析 设P(x,y),Q(x1,y1),F1(-c,0),F2(c,0),由$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,得x1=3c+2x,y1=2y…①
由$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,得x2-c2+y2=0,②又$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,③由②③可得P(-$\frac{a}{c}\sqrt{{b}^{2}+{c}^{2}}$,$\frac{{b}^{2}}{c}$),代入①得Q(3c-$\frac{2a\sqrt{{b}^{2}+{c}^{2}}}{c}$,$\frac{2{b}^{2}}{c}$),将点Q坐标代入③得3c2+a2=4a$\sqrt{{b}^{2}+{c}^{2}}$,即可求解.
解答 解:设P(x,y),Q(x1,y1),∵F1(-c,0),F2(c,0),
∴$\overrightarrow{Q{F_2}}$=(c-x1,-y1),$\overrightarrow{P{F_1}}$=(-c-x,-y)
∵$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,∴(c-x1,-y1)=2(-c-x,-y),
∴c-x1=2(-c-x),-y1=-2y,
∴x1=3c+2x,y1=2y…①
∴$\overrightarrow{{F}_{1}P}$=(x+c,y),$\overrightarrow{{F}_{2}P}$=(x-c,y),
∵$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,∴x2-c2+y2=0,②
又∵$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,③
由②③可得P(-$\frac{a}{c}\sqrt{{b}^{2}+{c}^{2}}$,$\frac{{b}^{2}}{c}$),代入①得Q(3c-$\frac{2a\sqrt{{b}^{2}+{c}^{2}}}{c}$,$\frac{2{b}^{2}}{c}$)
将点Q坐标代入③得3c2+a2=4a$\sqrt{{b}^{2}+{c}^{2}}$,⇒
9c4-26a2c2+17a4=0⇒9e4-26e2+17=0⇒
e2=1(舍去),e2=$\frac{17}{9}$⇒e=$\frac{\sqrt{17}}{3}$.
故选:B
点评 本题考查了双曲线的离心率,转化思想及运算能力是解题的关键,属于难题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
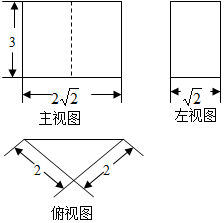
| A. | $(16+6\sqrt{2})c{{m}^{2}}^{\;}$ | B. | 22cm2 | C. | $(12+6\sqrt{2})c{m}^{2}$ | D. | $(18+2\sqrt{3})c{m}^{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com