
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2 ![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 .
,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 . 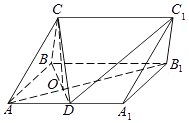
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
【答案】
(1)证明:∵D是矩形AA1的中点,∴AD= ![]() AA1=
AA1= ![]()
∴ ![]() =
= ![]() ,∴△DAB∽△ABB1,∴∠ABD=∠AB1B,
,∴△DAB∽△ABB1,∴∠ABD=∠AB1B,
∵∠BAB1+∠AB1B=90°,∴∠BAB1+∠ABD=90°,∴BD⊥AB1.
∵CO⊥平面ABB1A1,AB1平面ABB1A1,
∴CO⊥AB1,又CO平面BCD,BD平面BCD,CO∩BD=O,
∴AB1⊥平面BCD,∵CD平面BCD,
∴CD⊥AB1
(2)解:以O为原点,以OD,OB1,OC为坐标轴建立空间直角坐标系如图所示:
则A(0,﹣ ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0,0),C(0,0,
,0,0),C(0,0, ![]() ),D(
),D( ![]() ,0,0).
,0,0).
∴ ![]() =(
=( ![]() ,0,﹣
,0,﹣ ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ).
).
设平面ABC的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 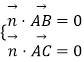 ,
,
即 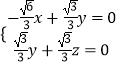 ,令x=1得
,令x=1得 ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() ).
).
∴ ![]() =
= ![]() ,∴cos<
,∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴直线CD与平面ABC所成角的正弦值为 ![]() .
.
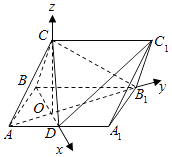
【解析】(1)根据线面垂直的性质定理得到线线垂直,再由线线垂直得到线面垂直进而得到线线垂直。(2)根据题意建立空间直角坐标系如图所示,求出各个点的坐标进而得到各个向量的坐标,找到平面ABC的法向量继而求出其与向量AD的数量积再根据数量积公式求出cos的值,进而可得直线CD与平面ABC所成角的正弦值。
【考点精析】通过灵活运用棱柱的结构特征和空间角的异面直线所成的角,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则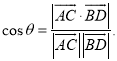 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,3,5,7},B={x|(2x﹣1)(x﹣5)>0},则A∩(RB)( )
A.{1,3}
B.{1,3,5}
C.{3,5}
D.{3,5,7}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品的市场需求量![]() (万件)、市场供应量
(万件)、市场供应量![]() (万件)与市场价格
(万件)与市场价格![]() (元/件)分别近似地满足下列关系:
(元/件)分别近似地满足下列关系: ![]() ,
, ![]() .当
.当![]() 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若该商品的市场销售量![]() (万件)是市场需求量
(万件)是市场需求量![]() 和市场供应量
和市场供应量![]() 两者中的较小者,该商品的市场销售额
两者中的较小者,该商品的市场销售额![]() (万元)等于市场销售量
(万元)等于市场销售量![]() 与市场价格
与市场价格![]() 的乘积.
的乘积.
①当市场价格![]() 取何值时,市场销售额
取何值时,市场销售额![]() 取得最大值;
取得最大值;
②当市场销售额![]() 取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数
是奇函数
(Ⅰ)求![]() 值;
值;
(Ⅱ)判断并证明该函数在定义域![]() 上的单调性;
上的单调性;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅳ)设关于![]() 的函数
的函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
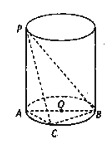
【题目】如图所示, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是圆柱底面圆的直径,
是圆柱底面圆的直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的任意一点,
的任意一点, ![]() .
.
(1)求证: ![]() ;
;
(2)求三棱锥![]() 体积的最大值,并写出此时三棱锥
体积的最大值,并写出此时三棱锥![]() 外接球的表面积.
外接球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点P(﹣3 ![]() ,4),它的渐近线方程为y=±
,4),它的渐近线方程为y=± ![]() x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com