
【题目】双曲线![]() =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图(1),在等腰直角![]() 中,斜边
中,斜边![]() ,D为
,D为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠得到如图(2)所示的三棱锥
折叠得到如图(2)所示的三棱锥![]() ,若三棱锥
,若三棱锥![]() 的外接球的半径为
的外接球的半径为![]() ,则
,则![]() _________.
_________.
图(1)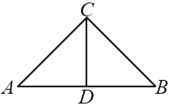 图(2)
图(2) 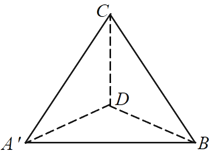
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市公益志愿者的年龄分布情况,有关部门通过随机抽样,得到如图1的频率分布直方图.
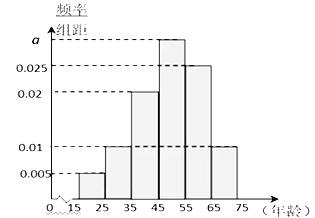
(1)求a的值,并估计该市公益志愿者年龄的平均数(同一组中的数据用该组区间的中点值作代表);
(2)根据世界卫生组织确定新的年龄分段,青年是指年龄15~44岁的年轻人.据统计,该市人口约为300万人,其中公益志愿者约占总人口的40%.试根据直方图估计该市青年公益志愿者的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,满足
,满足![]() ,且线段
,且线段![]() 与
与![]() 互相平分(
互相平分(![]() 为原点),求
为原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
(1)求直方图中a的值,并由频率分布直方图估计该单位职工一天步行数的中位数;
(2)若该单位有职工200人,试估计职工一天行走步数不大于13000的人数;
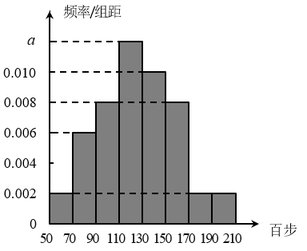
(3)在(2)的条件下,该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动,再从6人中选取2人担任领队,求这两人均来自区间(150,170]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 的周长为
的周长为![]()
(1)求椭圆![]() 的方程
的方程
(2)是否存在直线![]() ,使得
,使得![]() 为等腰直角三角形?若存在,求出直线的方程;若不存在,请说明理由
为等腰直角三角形?若存在,求出直线的方程;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的![]() 点处,乙船在中间
点处,乙船在中间![]() 点处,丙船在最后面的
点处,丙船在最后面的![]() 点处,且
点处,且![]() .一架无人机在空中的
.一架无人机在空中的![]() 点处对它们进行数据测量,在同一时刻测得
点处对它们进行数据测量,在同一时刻测得![]() ,
, ![]() .(船只与无人机的大小及其它因素忽略不计)
.(船只与无人机的大小及其它因素忽略不计)

(1)求此时无人机到甲、丙两船的距离之比;
(2)若此时甲、乙两船相距100米,求无人机到丙船的距离.(精确到1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com