【题目】如图，扇形的半径为r cm，周长为20cm，问扇形的圆心角α等于多少弧度时，这个扇形的面积最大，并求出扇形面积的最大值．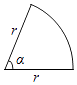 
【答案】解：设扇形的半径为r，弧长为l，则：l+2r=20，即l=20﹣2r（0＜r＜10）． 扇形的面积S= 
lr，将上式代入，得：S= （20﹣2r）r=﹣r2+10r=﹣（r﹣5）2+25，
所以：当且仅当r=5时，S有最大值25，
此时：l=20﹣2×5=10，α= 
=2rad．
所以：当α=2rad时，扇形的面积取最大值，最大值为25cm2
【解析】设扇形的半径为r，弧长为l，利用周长关系，表示出扇形的面积，利用二次函数求出面积的最大值，以及圆心角的大小．
【考点精析】本题主要考查了扇形面积公式的相关知识点，需要掌握若扇形的圆心角为
，半径为
，弧长为
，周长为
，面积为
，则
，
，
才能正确解答此题．
科目：高中数学 来源： 题型：
【题目】身穿红、黄两种颜色衣服的各有两人，身穿蓝颜色衣服的有一人，现将这五人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法共有（ ）
A. 24种 B. 28种 C. 36种 D. 48种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出以下说法：①不共面的四点中，任意三点不共线；
②有三个不同公共点的两个平面重合；
③没有公共点的两条直线是异面直线；
④分别和两条异面直线都相交的两条直线异面；
⑤一条直线和两条异面直线都相交，则它们可以确定两个平面．
其中正确结论的序号是_______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{xn}满足x1=1，x2=λ，并且 
=λ 
（λ为非零常数，n=2，3，4，…）． （Ⅰ）若x1 ， x3 ， x5成等比数列，求λ的值；
（Ⅱ）设0＜λ＜1，常数k∈N* ， 证明 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据下列条件求双曲线的标准方程：
(1)经过点(
，3)，且一条渐近线方程为4x＋3y＝0.
(2)P(0,6)与两个焦点的连线互相垂直，与两个顶点连线的夹角为
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2015高考山东文数】某中学调查了某班全部
名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
（1）从该班随机选
名同学，求该同学至少参加上述一个社团的概率；
（2）在既参加书法社团又参加演讲社团的
名同学中，有5名男同学
名女同学
现从这
名男同学和名女同学中各随机选
人，求
被选中且
未被选中的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
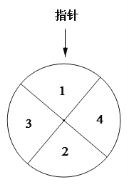
【题目】【2016高考山东文数】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次，每次转动后，待转盘停止转动时，记录指针所指区域中的数.设两次记录的数分别为x，y.奖励规则如下：
①若
，则奖励玩具一个；
②若
，则奖励水杯一个； ③其余情况奖励饮料一瓶.
假设转盘质地均匀，四个区域划分均匀.小亮准备参加此项活动.
（I）求小亮获得玩具的概率；
（II）请比较小亮获得水杯与获得饮料的概率的大小，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的极坐标方程为
，直线
的参数方程为
（
为参数， 
）.
（Ⅰ）把曲线
的极坐标方程化为直角坐标方程，并说明曲线
的形状；
（Ⅱ）若直线
经过点
，求直线
被曲线
截得的线段
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
