
【题目】已知p:x∈R,x2+2x≥a,q:x2﹣4x+3≤0,r:(x﹣m)[x﹣(m+1)]≤0.
(1)若命题p的否定是假命题,求实数a的取值范围;
(2)若q是r的必要条件,求实数m的取值范围.
【答案】(1) (﹣∞,﹣1],(2) [1,2].
【解析】
(1)由命题间的关系,即求命题![]() 为真时,
为真时,![]() 的取值范围,利用二次函数的性质,可求得结果;
的取值范围,利用二次函数的性质,可求得结果;
(1)求出命题![]() 为真时,
为真时,![]() 的集合,q是r的必要条件,转化为集合间关系,即可求出
的集合,q是r的必要条件,转化为集合间关系,即可求出![]() 的取值范围.
的取值范围.
p:x∈R,x2+2x≥a,q:x2﹣4x+3≤0,r:(x﹣m)[x﹣(m+1)]≤0,
∴根据二次函数的性质可知,x2+2x的最小值﹣1,
故P:a≤﹣1,
由x2﹣4x+3≤0可得1≤x≤3,
由(x﹣m)[x﹣(m+1)]≤0,可得m≤x≤m+1,
故q:A=[1,3],r:B=[m,m+1],
(1)若命题p的否定是假命题,即p为真命题,
故a的范围(﹣∞,﹣1],
(2)若q是r的必要条件,则rq,从而有BA,
∴![]() ,
,
解可得,1≤m≤2,
故m的范围[1,2].


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,点P是椭圆E上一点,满足
的左,右焦点,点P是椭圆E上一点,满足![]() 轴,
轴,![]() .
.
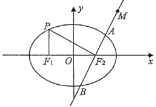
(1)求椭圆E的离心率;
(2)过点![]() 的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】6月12日,上海市发布了《上海市生活垃圾分类投放指南》,将人们生活中产生的大部分垃圾分为七大类.某幢楼前有四个垃圾桶,分别标有“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”,小明同学要将鸡骨头(湿垃圾)、贝壳(干垃圾)、指甲油(有害垃圾)、报纸(可回收物)全部投入到这四个桶中,若每种垃圾投放到每个桶中都是等可能的,那么随机事件“4种垃圾中至少有2种投入正确的桶中”的概率是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛,其中3名来自A学校且1名为女棋手,另外4名来自B学校且2名为女棋手![]() 从这7名队员中随机选派4名队员参加第一阶段的比赛
从这7名队员中随机选派4名队员参加第一阶段的比赛
![]() 求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
![]() Ⅱ
Ⅱ![]() 设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望
设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为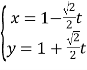 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是一种反映和评价空气质量的方法,
是一种反映和评价空气质量的方法,![]() 指数与空气质量对应如下表所示:
指数与空气质量对应如下表所示:

如图是某城市2018年12月全月的指![]() 数变化统计图.
数变化统计图.
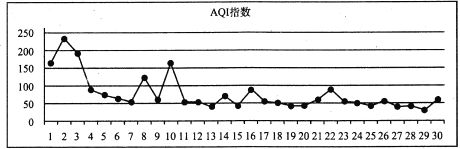
根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半月的空气质量
C. 从![]() 数据看,前半月的方差大于后半月的方差
数据看,前半月的方差大于后半月的方差
D. 从![]() 数据看,前半月的平均值小于后半月的平均值
数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com