
【题目】已知数列![]() 是等比数列,
是等比数列, ![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)设![]() 且
且![]() 为递增数列.若
为递增数列.若![]() 求证:
求证: ![]()
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】为及时了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位30岁到40岁的公务员,得到情况如下表:
(1)判断是否有99%以上的把握认为“生二胎意愿与性别有关”,并说明理由;
(2)现把以上频率当作概率,若从社会上随机独立抽取三位30岁到40岁的男公务员访问,求这三人中至少有一人有意愿生二胎的概率.
(3)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省女联的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 30 | 15 | 45 |
无意愿生二胎 | 20 | 25 | 45 |
总计 | 50 | 40 | 90 |
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
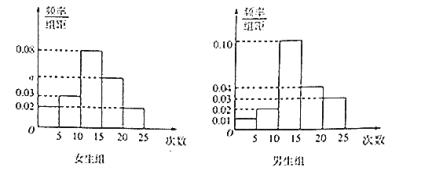
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取3人 ,并用![]() 表示其中男生的人数,求
表示其中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
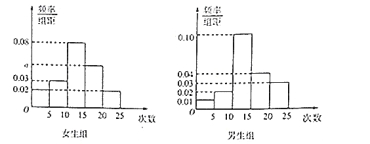
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(1)写出![]() 的值;
的值;
(2)求抽取的40名学生中月上网次数不少于15次的学生人数;
(Ⅲ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人 ,求至少抽到1名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
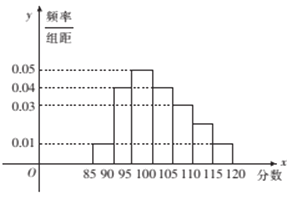
【题目】某校高二奥赛班![]() 名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100-110的学生数有21人.
名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100-110的学生数有21人.
(1)求总人数![]() 和分数在110-115分的人数
和分数在110-115分的人数![]() ;
;
(2)现准备从分数在110-115的![]() 名学生(女生占
名学生(女生占![]() )中任选3人,求其中恰好含有一名女生的概率;
)中任选3人,求其中恰好含有一名女生的概率;
(3)为了分析某个学生的学习状态,对其下一阶段的学生提供指导性建议,对他前7次考试的数学成绩![]() (满分150分),物理成绩
(满分150分),物理成绩![]() 进行分析,下面是该生7次考试的成绩.
进行分析,下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() ,
,![]() ……
……![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: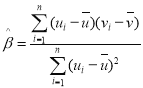 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() .
.

(1)在![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求
,并求![]() 的值;
的值;
(2)在(1)条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com