
分析 (Ⅰ)根据新定义即可求出a2=(6,0)或(0,4),
(Ⅱ)利用反证法即可证明,
(Ⅲ)由新定义可得kmin=5,相应的a1,a2,…,ak.
解答 解:(Ⅰ)对于任意的b=(x2,y2)∈D,a1+b=(0,0)+(x2,y2)=(x2,y2)
若(x2,y2)∈Ω,则(x2,y2)=(6,0),或(x2,y2)=(0,4),
故a2=(6,0)或(0,4),
(Ⅱ) 证明:假设命题不成立,即?k∈N*,使ak=(5,0)
即?bi∈D,i=1,2,…,k-1(k≥2),使a1+$\sum_{i=1}^{k-1}{b}_{i}$=ak,化简得$\sum_{i=1}^{k-1}{b}_{i}$=(5,0),
所以存在m,n,p∈Z,且m+n+p=k-1,使6m+4n+2p=5.
又因为6m+4n+2p=2(3m+2n+p)是偶数,而5是奇数,与6m+4n+2p=5矛盾,
故假设不成立,即:?k∈N*,ak≠(5,0),
(Ⅲ)kmin=5,a1=(0,0),a2=(0,4),a3=(4,0),a4=(4,4),a5=(6,2).
点评 本题考查了新定义的知识的应用,关键是读懂新定义,以及反证法,属于中档题.


科目:高中数学 来源: 题型:选择题
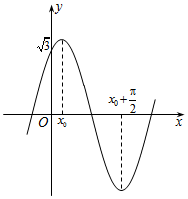 已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则函数f(x)的解析式的值为( )
已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则函数f(x)的解析式的值为( )| A. | $f(x)=2sin(2x+\frac{π}{6})$ | B. | $f(x)=2sin(2x+\frac{π}{3})$ | C. | $f(x)=2sin(x+\frac{π}{6})$ | D. | $f(x)=2sin(x+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
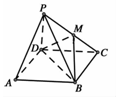 已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上
已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com