
分析 可画出图形,连接AP并延长交BC于D,连接BP交AC于E,连接CP交AB于F,然后过A作BE的平行线,交CF的延长线于M,作CF的平行线,交BE延长线于N,从而得到平行四边形AMPN,根据相似三角形对应边的比例关系可以得到$\frac{AM}{PB}=\frac{AF}{FB},\frac{AN}{PC}=\frac{AE}{EC}$,从而得到$\overrightarrow{AP}=\frac{AF}{FB}•\overrightarrow{PB}+\frac{AE}{EC}•\overrightarrow{PC}$.可以说明S△PCA:S△PBC=AF:FB,S△PAB:S△PBC=AE:EC,这样便可得出${S}_{△PAB}•\overrightarrow{PC}+{S}_{△PBC}•\overrightarrow{PA}+{S}_{△PCA}•\overrightarrow{PB}=\overrightarrow{0}$.
解答 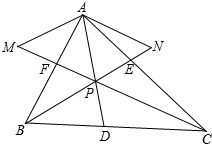 解:如图,连接AP,并延长AP交BC于D,连结BP并延长交AC于E,连结CP并延长交AB于F,过A作AM∥BE交CF延长线于M,作AN∥CF交BE延长线于N,则四边形AMPN为平行四边形;
解:如图,连接AP,并延长AP交BC于D,连结BP并延长交AC于E,连结CP并延长交AB于F,过A作AM∥BE交CF延长线于M,作AN∥CF交BE延长线于N,则四边形AMPN为平行四边形;
∴$\overrightarrow{AP}=\overrightarrow{AM}+\overrightarrow{AN}$,且△AMF∽△BPF;
∴$\frac{AM}{PB}=\frac{AF}{FB}$;
同理,$\frac{AN}{PC}=\frac{AE}{EC}$;
∴$\overrightarrow{AM}=\frac{AF}{FB}•\overrightarrow{PB},\overrightarrow{AN}=\frac{AE}{EC}•\overrightarrow{PC}$;
∴$\overrightarrow{AP}=\frac{AF}{FB}•\overrightarrow{PB}+\frac{AE}{EC}•\overrightarrow{PC}$;
∵△PCA和△PBC有公共的底边PC,设它们的高分别为h1,h2,则:
S△PAC:S△PBC=h1:h2=AF:FB,同理S△PAB:S△PBC=AE:EC;
∴$\overrightarrow{AP}=\frac{{S}_{△PAC}}{{S}_{△PBC}}•\overrightarrow{PB}+\frac{{S}_{△PAB}}{{S}_{△PBC}}•\overrightarrow{PC}$;
∴${S}_{△PAB}•\overrightarrow{PC}+{S}_{△PBC}•\overrightarrow{PA}+{S}_{△PCA}•\overrightarrow{PB}=\overrightarrow{0}$.
点评 考查数形结合解题的方法,向量加法的平行四边形法则,相似三角形的判断及对应边的比例关系,向量数乘的几何意义,以及三角形的面积公式,向量的数乘运算.


科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤3} | B. | {x|-2≤x<-1} | C. | {x|3≤x<4} | D. | {x|x≤3或x>4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 正三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
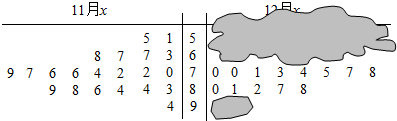
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com