
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 连结BF,取BF中点O,连结EO、CO,则∠OEC是直线CE,AF的夹角(或夹角的补角),由此能求出直线CE,AF的夹角的余弦值.
解答 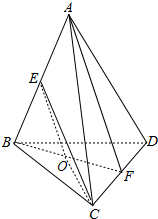 解:连结BF,取BF中点O,连结EO、CO,设正四面体棱长为2,
解:连结BF,取BF中点O,连结EO、CO,设正四面体棱长为2,
∵在正四面体A-BCD中,E,F分别是线段AB,CD的中点,
∴EO∥AF,∴∠OEC是直线CE,AF的夹角(或夹角的补角),
AF=CE=BF=$\sqrt{4-1}=\sqrt{3}$,EO=FO=$\frac{\sqrt{3}}{2}$,
CO=$\sqrt{(\frac{\sqrt{3}}{2})^{2}+{1}^{2}}$=$\frac{\sqrt{7}}{2}$,
∴cos∠OEC=$\frac{\frac{3}{4}+3-\frac{7}{4}}{2×\frac{\sqrt{3}}{2}×\sqrt{3}}$=$\frac{2}{3}$.
∴直线CE,AF的夹角的余弦值是$\frac{2}{3}$.
故选:D.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
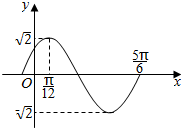 函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| B. | 命题“若x=y,则sin x=sin y”的逆否命题为真命题 | |
| C. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| D. | 命题“?x∈R,使得:x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com