
【题目】如图所示,M、N、K分别是正方体ABCD﹣A1B1C1D1的棱AB,CD,C1D1的中点.求证:
(1)AN∥平面A1MK;
(2)MK⊥平面A1B1C.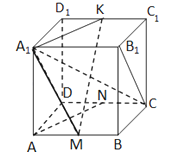
【答案】证明:(1)连接KN,由于K、N为CD,C1D1的中点,
所以KN平行且等于AA1 ,
AA1KN为平行四边形AN∥A1K,
而A1K平面A1MK,AN平面A1MK,
从而AN∥平面A1MK.
(2)连接BC1 , 由于M、K为AB、C1D1的中点,
所以:KC1与MB平行且相等,
从而:KC1MB为平行四边形,
所以:MK∥BC1 ,
而:BC1⊥B1C,BC1⊥A1B1 ,
从而:BC1⊥平面A1B1C,
所以:MK⊥平面A1B1C.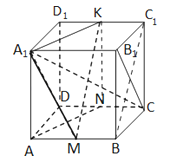
【解析】(1),要证明AN∥平面A1MK,只需证明AN平行于平面A1MK内的一条直线,容易证明AN∥A1K,从而得证;
(2),要证明平面A1B1C⊥MK,只需证明BC1⊥平面A1B1C,BC1∥MK即可,从而问题得以解决.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为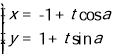 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为了对房地产市场进行调控决策,统计部门对外来人口和当地人口进行了买房的心理预期调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表(不全):
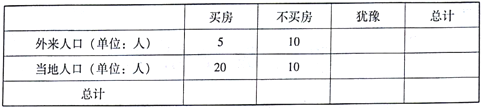
已知样本中外来人口数与当地人口数之比为3:8.
(1)补全上述列联表;
(2)从参与调研的外来人口中用分层抽样方法抽取6人,进一步统计外来人口的某项收入指标,若一个买房人的指标记为3,一个犹豫人的指标记为2,一个不买房人的指标记为1,现在从这6人中再随机选取3人,求选取的3人的指标之和大于5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是:P=![]()
该商品的日销售量Q(件)与时间t(天)的函数关系是:Q=﹣t+40(0<t≤30,t∈N*),求这种商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点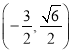 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中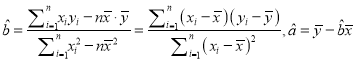 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com