
| A. | 9 | B. | 7 | C. | 5 | D. | 3 |
分析 根据已知可得ω为正奇数,且ω≤8,结合条件进行验证,可得ω的最大值.
解答 解:∵x=-$\frac{π}{8}$是y=f(x)的零点,直线x=$\frac{3π}{8}$为y=f(x)图象的一条对称轴,
∴$\frac{2n+1}{4}•T$=$\frac{π}{2}$,(n∈N)
即ω=$\frac{2π}{T}$=2n+1,(n∈N)
即ω为正奇数,
∵函数f(x)在区间($\frac{π}{12}$,$\frac{5π}{24}$)上单调,
∴$\frac{5π}{24}$-$\frac{π}{12}$=$\frac{π}{8}$≤$\frac{T}{2}$
即T=$\frac{2π}{ω}≥\frac{π}{4}$,解得:ω≤8,
当ω=7时,-$\frac{7π}{8}$+φ=kπ+$\frac{π}{2}$,k∈Z,
取φ=$\frac{3π}{8}$,
此时f(x)在($\frac{π}{12}$,$\frac{5π}{24}$)不单调,不满足题意;
当ω=5时,-$\frac{5π}{8}$+φ=kπ+$\frac{π}{2}$,k∈Z,
取φ=$\frac{π}{8}$,
此时f(x)在($\frac{π}{12}$,$\frac{5π}{24}$)不单调,满足题意;
当ω=3时,-$\frac{3π}{8}$+φ=kπ+$\frac{π}{2}$,k∈Z,
取φ=-$\frac{π}{8}$,
此时f(x)在($\frac{π}{12}$,$\frac{5π}{24}$)单调,满足题意;故ω的最大值为3,
故选:D.
点评 本题考查的知识点是正弦型函数的图象和性质,本题转化困难,难度较大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
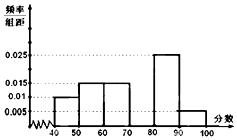 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p:?x∈R,ex>xe,q:?x0∈R,|x0|≤0,则(¬p)∧q为假 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
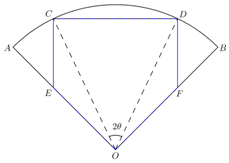 现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.
现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
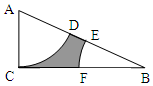 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
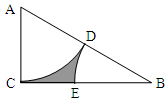 如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | 1-$\frac{{\sqrt{3}π}}{6}$ | B. | $\frac{{\sqrt{3}π}}{6}$ | C. | 1-$\frac{π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com