【题目】为推行“新课堂”教学法，某老师在甲乙两个班分别用传统教学和“新课堂”两种不同的教学方式进行教学实验.为了解教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图(如下图所示)，记成绩不低于70分者为“成绩优良”.
（1）分别计算甲乙两班20个样本中，分数前十的平均分，并据此判断哪种教学方式的教学效果更佳；
（2）甲乙两班40个样本中，成绩在60分以下的学生中任意选取2人，求这2人来自不同班级的概率.
【答案】（1）
，
，“新课堂”教学方式；（2）
.
【解析】
（1）分别求出甲班样本中分数前十的平均分和乙班样本中分数前十的平均分，由甲班样本中分数前十的平均分低于乙班样本中分数前十的平均分，得出“新课堂”教学方式的教学效果更佳；
（2）样本中成绩60分以下的学生中甲班有4人，记为：
，
，
，
，乙班有2人，记为：1，2.然后利用列举法能求出结果.
（1）甲班样本中成绩前十的平均分为
.
乙班样本中成绩前十的平均分为
.
甲班样本成绩前十的平均分远低于乙班样本成绩前十的平均分，大致可以判断“新课堂”教学方式的教学效果更佳；
（2）样本中成绩60分以下的学生中甲班有4人，记为：，，，，乙班有2人，记为：1，2.
则从，，，，1，2六个元素中任意选2个的所有基本事件如下：
，
，
，
，
，
，
，
，
，
，
，
，
，
，12，一共有15个基本事件，
设
表示“这2人来自不同班级”有如下：，，，，，，，，一共有8个基本事件，
所以
.
科目：高中数学 来源： 题型：
【题目】如图，矩形ABCD的两条对角线相交于点M(2，0)，AB边所在直线的方程为x－3y－6＝0，点T(－1，1)在AD边所在直线上．求：
(1) AD边所在直线的方程；
(2) DC边所在直线的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：
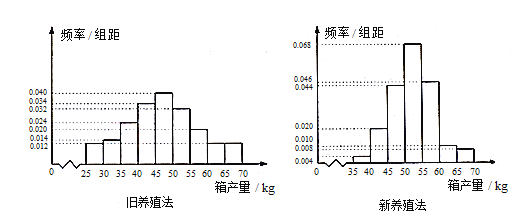
（1）记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】要得到函数
的图象, 只需将函数
的图象（ ）
A. 所有点的横坐标伸长到原来的2倍(纵坐标不变), 再将所得的图像向左平移
个单位.
B. 所有点的横坐标伸长到原来的2倍(纵坐标不变), 再将所得的图像向左平移
个单位.
C. 所有点的横坐标缩短到原来的
倍(纵坐标不变), 再将所得的图像向左平移个单位.
D. 所有点的横坐标缩短到原来的倍(纵坐标不变), 再将所得的图像向左平移个单位.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，四棱锥P－ABCD中，AP⊥平面PCD，AD∥BC，AB＝BC＝
AD，E，F分别为线段AD，PC的中点.
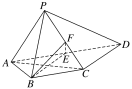
(1)求证：AP∥平面BEF；
(2)求证：BE⊥平面PAC.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）直接写出
的零点；
（2）在坐标系中，画出的示意图（注意要画在答题纸上）
（3）根据图象讨论关于
的方程
的解的个数:
（4）若方程，有四个不同的根
、
、
、
直接写出这四个根的和；
（5）若函数在区间
上既有最大值又有最小值，直接写出a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
