
 =0,求以OA、OB为直径的两圆的另一个交点P的轨迹.
=0,求以OA、OB为直径的两圆的另一个交点P的轨迹.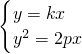 ,解得A(
,解得A(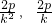 )
) ,知OA⊥OB,所以OB的方程为y=-
,知OA⊥OB,所以OB的方程为y=- x
x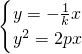 ,解得B(2pk2,-2pk)
,解得B(2pk2,-2pk)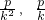 ),OB的中点为B'(pk2,-pk)
),OB的中点为B'(pk2,-pk)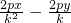 =0 …①
=0 …① )x …③
)x …③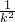 -1)=2p …④
-1)=2p …④

科目:高中数学 来源: 题型:
 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若 | OM |
| OA |
| ON |
| OB |
| NM |
| MP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,设Ox,Oy是平面内相交成60°角的两条数轴,
如图,设Ox,Oy是平面内相交成60°角的两条数轴,| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
| OA |
| OB |
| e1 |
| OA |
| e1 |
| OB |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•成都一模)如图,设A、B、C是球O面上的三点,我们把大圆的劣弧
(2010•成都一模)如图,设A、B、C是球O面上的三点,我们把大圆的劣弧 |
| BC |
 |
| CA |
 |
| AB |
 |
| BC |
 |
| CA |
 |
| AB |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
 |
| AB |
 |
| CA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com