已知圆C的圆心在直线y=x+1上,且过点A(1,3),与直线x+2y-7=0相切.
(1)求圆C的方程;
(2)设直线l:ax-y-2=0(a>0)与圆C相交于A、B两点,求实数a的取值范围.
【答案】
分析:(1)设圆心C(a,b),由圆C的圆心在直线y=x+1上,且过点A(1,3),与直线x+2y-7=0相切,建立方程组求出圆心和半径,由此能求出圆C的方程.
(2)把直线y=ax-2代入圆的方程,得(a
2+1)x
2-6ax+4=0,由直线ax-y+5=0交圆于A,B两点,知5a
2-4>0,由此能求出实数a的取值范围.
解答:解:(1)设圆心C(a,b),
∵圆C的圆心在直线y=x+1上,且过点A(1,3),与直线x+2y-7=0相切,
∴
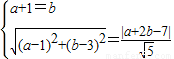
,
解得a=0,b=1,
∴圆心C(0,1),圆半径r=|AC|=
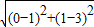
=
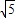
,
∴圆C的方程为x
2+(y-1)
2=5.(8分)
(2)把直线ax-y-2=0,即y=ax-2代入圆的方程x
2+(y-1)
2=5,
消去y整理,得(a
2+1)x
2-6ax+4=0,
∵直线ax-y+5=0交圆于A,B两点,
∴△=36a
2-16(a
2+1)>0.即5a
2-4>0,
由于a>0,解得a>
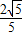
.
所以实数a的取值范围是(
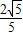
,+∞). (15分)
点评:本题考查圆的方程的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

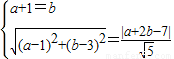 ,
,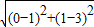 =
=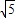 ,
,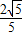 .
.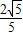 ,+∞). (15分)
,+∞). (15分)
