
【题目】设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)<0,试判断y=f(x)的单调性并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;
(3)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
【答案】
(1)解:∵f(x)是定义域为R的奇函数,∴f(0)=0,
∴1﹣(k﹣1)=0,∴k=2
(2)解:f(x)=ax﹣a﹣x(a>0且a≠1),
若f(1)<0,则a﹣ ![]() <0,
<0,
∵a>0且a≠1,
∴a2﹣1<0,即0<a<1
∵ax单调递减,a﹣x单调递增,
故f(x)在R上单调递减.
不等式化为f(x2+tx)<f(x﹣4),
∴x2+tx>x﹣4,即x2+(t﹣1)x+4>0恒成立
∴△=(t﹣1)2﹣16<0,解得﹣3<t<5
(3)解: ![]() ,
,
∴ ![]() ,
,
∴ ![]()
g(x)=22x+2﹣2x﹣2(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2(2x﹣2﹣x)+2
令t=2x﹣2﹣x
∵t=2x﹣2﹣x在[1,+∞)上为递增的,
∴ ![]()
∴设h(t)=t2﹣2t+2=(t﹣1)2+1, ![]()
∴ ![]() ,
,
即g(x)在[1,+∞)上的最小值为 ![]()
【解析】(1)根据函数奇偶性的定义和性质进行求解即可.(2)根据不等式求出a的取值范围,判断函数的单调性,将不等式恒成立进行转化即可.(3)利用换元法,结合一元二次函数单调性的性质进行求解即可.


科目:高中数学 来源: 题型:
【题目】如图所示的函数F(x)的图象,由指数函数f(x)=ax与幂函数g(x)=xb“拼接”而成. 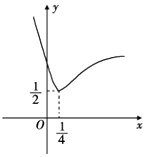
(1)求F(x)的解析式;
(2)比较ab与ba的大小;
(3)已知(m+4)﹣b<(3﹣2m)﹣b , 求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2mx+3m+4,
(1)若f(x)在(﹣∞,1]上单调递减,求m的取值范围;
(2)求f(x)在[0,2]上的最大值g(m).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①定义在R上的函数f(x)满足f(﹣2)=f(2),则f(x)不是奇函数
②定义在R上的函数f(x)恒满足f(﹣x)=|f(x)|,则f(x)一定是偶函数
③一个函数的解析式为y=x2 , 它的值域为{0,1,4},这样的不同函数共有9个
④设函数f(x)=lnx,则对于定义域中的任意x1 , x2(x1≠x2),恒有 ![]() ,
,
其中为真命题的序号有(填上所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直线坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为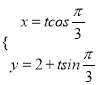 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 在
在![]() 上,
上, ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个周期后,所得图象对应的函数为( )
个周期后,所得图象对应的函数为( )
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin(2x﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com